2lk Matematiikka - Tekninen opas
Lataa tekninen opas pdf-tiedostona (516kB, 8.9.2014)
Viiteaineiston kuvaus
Viitejoukko
Viitejoukko koostui syksyn matematiikan tehtävissä 27 arvioitsijasta ja 622 oppilaasta. Talvella arvioitsijoita oli 28 ja lapsia yhteensä 527. Keväällä arvioitsijoita oli yhteensä 25 ja arvioitavia lapsia 531. Yleisimmin arvioinnin oli tehnyt toisen luokan opettaja omalle ryhmälleen, mutta joissain tapauksissa sama opettaja oli teettänyt tehtävät useammalle luokalle. Mukaan tulleet luokat valikoituivat opettajien vapaaehtoisen ilmoittautumisen perusteella. Maantieteellisesti luokat sijoittuivat eri puolille Suomea painottuen Keski-Suomen maakuntaan ja otos sisälsi sekä isoja että pieniä kuntia. Yleisperiaatteena oli, että kaikki luokan lapset tekivät kaikki tehtävät, eikä yksittäisiä erityisoppilaita poistettu otoksesta. Kaikki mukana olleet luokat osallistuivat normaaliin perusopetukseen, erityisluokkia tai pienryhmiä ei otettu mukaan aineiston keruuseen. Kaiken kaikkiaan viiteaineisto on riittävän suuri ja ikä- sekä luokkatasoa hyvin edustava, niin että viitearvoja voidaan pitää luotettavina.
Taulukossa 1 on esitetty viiteaineistojen koot kolmessa eri ajankohdassa sukupuolittain ryhmiteltynä sekä ikäkeskiarvot ja keskihajonnat. Syksyn aineistoon kuului 14 lasta, jotka olivat vuotta vanhempia, eli olivat aloittaneet ensimmäisen luokan vuoden muita myöhemmin tai ovat vuosiluokan kerranneita oppilaita. Talvella vuotta vanhempia oppilaita oli 29 ja keväällä 26.
| Ikä | ||||
|---|---|---|---|---|
| tyttöjä | poikia | keskiarvo | keskihajonta | |
| Syksy | 314 | 308 | 8v 2kk | 3,9kk |
| Talvi | 264 | 263 | 8v 8kk | 4,4kk |
| Kevät | 259 | 272 | 8v 11kk | 4,0kk |
Aineistonkeruu
Viiteaineisto kerättiin vuonna 2011 kolmena ajankohtana: syksyllä (elo-syyskuussa), talvella (tammi-helmikuussa) ja keväällä (huhti-toukokuussa). Syksystä kevääseen ulottuvaa seuranta-aineistoa ei saatu, koska syksyn aineisto kerättiin talven ja kevään aineistonkeruun jälkeen ja osallistujina olivat tällöin eri lapset kuin talvella ja keväällä. Pääsääntöisesti tehtävät esitti opettaja annettujen kirjallisten ohjeiden mukaisesti. Opettajan ollessa estynyt, aineiston keräsi Niilo Mäki Instituutin kouluttama testaaja. Tehtävät pisteitettiin Niilo Mäki Instituutissa. Ryhmäarviointitehtävien teko syksyllä kesti noin 40 minuuttia. Talven tehtävien tekemiseen kului aikaa noin 35 minuuttia kun taas kevään tehtävät tehtiin noin 50 minuutissa. Ryhmäarviointi tehtiin pääsääntöisesti koko luokalle kerrallaan, mutta tarvittaessa opettaja saattoi jakaa luokkansa pienempiin ryhmiin. Tyypillisimmin kunkin ajankohdan kaikki tehtävät tehtiin yhden päivän aikana.
Tehtävien kuvaukset
Syksyllä arvioitiin matematiikan perustaitoja kaikkiaan kuudella, talvella seitsemällä ja keväällä kymmenellä eri tehtävällä, jotka teetettiin ryhmäarviointitilanteessa. Kaikissa tehtävissä, sekä syksyllä, talvella että keväällä, mittana käytettiin oikeiden vastausten summapistemäärää. Tehtävät ja niiden osiot valittiin niin, että eri arviointiajankohtina arvioinnin kohteena olisivat sillä hetkellä kehittymässä tai opetuksen painopisteessä olevat taidot. Syksyllä keskityttiin peruslaskutaidon sujuvuuteen lukualueella 1-20 sekä lukujen tuottamiseen ja ymmärtämiseen. Toisen luokan talvella ja keväällä edelleen arvioidaan perus yhteen- ja vähennyslaskutaidon sujuvuutta, mutta sen rinnalla painopiste siirtyi enemmän moninumeroisilla luvuilla laskemiseen ja samalla lukujärjestelmätiedon soveltamisen laskemisessa.
Syksyn tehtävät
Lukumääräisyyden tajua arvioiva tehtävä
Lukumääräisyyden tajua arvioidaan Lukujen suuruusvertailun tehtävällä.
Lukujen suurusvertailun tehtävässä lapsen tulee valita annetuista luvuista suurin tai pienin. Syksyllä vertaillaan kymmen– ja satalukuja. Opettaja osoittaa ensimmäisen rivin lukuja (61 59 48 63) ja sanoo: ”Tässä on lukuja. Katso huolellisesti kaikki luvut. Mikä näistä on suurin luku? Rastita oikea vastaus”. Opettaja ohjeistaa samalla tavalla toisen kohdan, jonka jälkeen oppilas tekee tehtäväsivun loppuun. Seuraavalla sivulla oppilaalla on neljä vastaavanlaista tehtäväkohtaa, mutta nyt oppilasta ohjeistetaan valitsemaan pienin luku. Suuruusvertailun tehtävässä on kaikkiaan 8 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos rasti puuttui, oli väärän luvun päällä tai rasteja oli osiossa enemmän kuin yksi, annettiin nolla pistettä.
Matemaattisten suhteiden hallintaa arvioiva tehtävä
Matemaattisten suhteiden hallinnan taitoryppäästä arvioidaan matemaattis-loogisia taitoja, ja tarkemmin sarjoittamisen osataitoa.
Sarjoittamisen tehtävässä arvioidaan lukujonon hallintaa lukualueella 1-70. Lapsella on edessään tehtäväpaperi, jossa on laatikkoja, joissa kussakin on kolme lukua (esim. 3,5,7). Opettaja osoittaa lukuja ja sanoo ”Katso näitä lukuja. Keksitkö, mikä luku tulee tähän tyhjälle viivalle? Kirjoita luku viivalle." Opettaja ohjeistaa samalla tavalla toisen kohdan, jonka jälkeen oppilas tekee tehtäväsivun loppuun. Sarjoittamisen tehtävässä on kaikkiaan 8 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Laskemisen taitoa arvioiva tehtävä
Laskemisen taidon ryppäästä arvioidaan numerosymbolien hallintaa.
Numerosymbolien hallinnan tehtävässä lapsen tulee kirjoittaa numeroin sanottu luku. Lukualue on 10–220. Lapsella on edessään tehtäväpaperi, jossa on laatikkoja, joissa kussakin on kolme lukua (esim. 3, 5, 7). Opettaja osoittaa lukuja ja sanoo: "Tässä tehtävässä sanon lukuja. Kirjoita luku numeroin kuvan viereen. Aloitetaan." Numerosymbolien hallinnan tehtävässä on kaikkiaan 8 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Aritmeettisia perustaitoja arvioivat tehtävät
Aritmeettisten perustaitojen ryppäästä arvioidaan yhteen- ja vähennyslaskun sujuvuutta.
Yhteenlaskun sujuvuus –tehtävässä lapsen tulee ratkaista niin monta laskua kuin mahdollista yhden minuutin aikana. Lukualue on 1–20. Ohjeistuksen aikana lapsen tulee pysyä STOP –merkillä kuvitetulla odota –sivulla. Opettaja näyttää tehtävälomakkeesta laskutehtävää ja sanoo: ”Seuraavaksi näet yhteenlaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Laske laskut ylhäältä alas. Aloita harmaasta sarakkeesta ja jatka sitten valkoiseen. Laske tehtäviä niin pitkälle kuin ehdit.”
”Kun annan luvan, voit kääntää sivua ja aloittaa tehtävän. Heti, kun sanon SEIS, lopeta tehtävä ja laita kynä pöydälle. Laske mahdollisimman nopeasti ja tarkasti. No niin, ota kynä käteen ja käännä sivua. ALOITA.” Kun yksi minuutti on kulunut opettaja sanoo: ”SEIS. Hyvä, laita kynä pöydälle ja käännä seuraava sivu.”
Yhteenlaskutehtävässä on kaikkiaan 20 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä. Lopuksi lapsen saama pistemäärä puolitetaan, eli tehtävän maksimipistemäärä on 10.
Vähennyslaskun sujuvuus –tehtävä on ohjeistukseltaan yhteenlaskutehtävän kanssa identtinen. Lapsen tulee ratkaista niin monta laskua kuin mahdollista yhden minuutin aikana. Lukualue on 1–20. Ohjeistuksen aikana lapsen tulee pysyä STOP –merkillä kuvitetulla odota –sivulla. Opettaja näyttää tehtävälomakkeesta laskutehtävää ja sanoo: ”Seuraavaksi näet vähennyslaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Laske laskut ylhäältä alas. Aloita harmaasta sarakkeesta ja jatka sitten valkoiseen. Laske tehtäviä niin pitkälle kuin ehdit.”
”Kun annan luvan, voit kääntää sivua ja aloittaa tehtävän. Heti, kun sanon SEIS, lopeta tehtävä ja laita kynä pöydälle. Laske mahdollisimman nopeasti ja tarkasti. No niin, ota kynä käteen ja käännä sivua. ALOITA.” Kun yksi minuutti on kulunut opettaja sanoo: ”SEIS. Hyvä, laita kynä pöydälle ja käännä seuraava sivu.”
Vähennyslaskutehtävässä on kaikkiaan 20 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä. Lopuksi lapsen saama pistemäärä puolitetaan, eli tehtävän maksimipistemäärä on 10.
Lukujärjestelmätiedon soveltamista laskemisessa arvioiva tehtävä
Lukujärjestelmätiedon soveltamista laskemisessa arvioidaan rahojen yhteenlaskua sisältävällä tehtävällä.
Tehtävässä lapsen tulee laskea rahoja yhteen. Lukualue on 1–120. Lapsella on edessään tehtäväpaperi, jossa on kahdessa sarakkeessa yhteensä kahdeksan ruutua, joissa on rahoja. Opettaja näyttää tehtävälomakkeesta ensimmäistä ruutua ja sanoo: "Tässä on rahoja. Laske, kuinka paljon rahaa on yhteensä ja kirjoita vastaus numeroin viivalle. Laske myös muut tehtävät. Aloita harmaasta sarakkeesta ja jatka sitten valkoiseen. Nyt voit tehdä tämän sivun loppuun. Laita kynä pöydälle, kun olet valmis." Tehtävässä on kaikkiaan 8 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Talven tehtävät
Lukumääräisyyden tajua arvioiva tehtävä
Lukumääräisyyden tajua arvioidaan Lukujen suuruusvertailun tehtävällä.
Lukujen suurusvertailun tehtävässä lapsen tulee valita annetuista luvuista suurin. Talvella vertaillaan kymmen– ja satalukuja. Opettaja osoittaa ensimmäisen rivin lukuja (66 91 78 89) ja sanoo: ”Tässä on lukuja Katso huolellisesti kaikki luvut. Mikä näistä on suurin luku? Rastita oikea vastaus”. Tämän jälkeen oppilas tekee tehtäväsivun loppuun. Suuruusvertailun tehtävässä on kaikkiaan 4 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos rasti puuttui, oli väärän luvun päällä tai rasteja oli osiossa enemmän kuin yksi, annettiin nolla pistettä.
Aritmeettisia perustaitoja arvioivat tehtävät
Aritmeettisten perustaitojen ryppäästä arvioidaan yhteen- ja vähennyslaskun sujuvuutta lukualueella 1–20 sekä päässä- ja allekkainlaskua lukualueella 20–100.
Yhteenlaskun sujuvuus –tehtävässä lapsen tulee ratkaista niin monta laskua kuin mahdollista yhden minuutin aikana. Lukualue on 1–20. Lapsella on edessään tehtäväpaperi. Ohjeistuksen aikana lapsen tulee pysyä STOP –merkillä varustetulla odota –sivulla. Opettaja näyttää tehtävälomakkeesta laskutehtävää ja sanoo: ”Seuraavaksi näet yhteenlaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Laske laskut ylhäältä alas. Aloita harmaasta sarakkeesta ja jatka sitten valkoiseen. Laske tehtäviä niin pitkälle kuin ehdit.”
”Kun annan luvan, voit kääntää sivua ja aloittaa tehtävän. Heti, kun sanon SEIS, lopeta tehtävä ja laita kynä pöydälle. Laske mahdollisimman nopeasti ja tarkasti. No niin, ota kynä käteen ja käännä sivua. ALOITA.” Kun yksi minuutti on kulunut opettaja sanoo: ”SEIS. Hyvä, laita kynä pöydälle ja käännä seuraava sivu.”
Yhteenlaskutehtävässä on kaikkiaan 20 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä. Lopuksi lapsen saama pistemäärä puolitetaan, eli tehtävän maksimipistemäärä on 10.
Vähennyslaskun sujuvuus –tehtävä on ohjeistukseltaan yhteenlaskutehtävän kanssa identtinen. Lapsen tulee ratkaista niin monta laskua kuin mahdollista yhden minuutin aikana. Lukualue on 1–20. Lapsella on edessään tehtäväpaperi. Ohjeistuksen aikana lapsen tulee pysyä STOP –merkillä kuvitetulla odota –sivulla. Opettaja näyttää tehtävälomakkeesta laskutehtävää ja sanoo: ”Seuraavaksi näet vähennyslaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Laske laskut ylhäältä alas. Aloita harmaasta sarakkeesta ja jatka sitten valkoiseen. Laske tehtäviä niin pitkälle kuin ehdit.”
”Kun annan luvan, voit kääntää sivua ja aloittaa tehtävän. Heti, kun sanon SEIS, lopeta tehtävä ja laita kynä pöydälle. Laske mahdollisimman nopeasti ja tarkasti. No niin, ota kynä käteen ja käännä sivua. ALOITA.” Kun yksi minuutti on kulunut opettaja sanoo: ”SEIS. Hyvä, laita kynä pöydälle ja käännä seuraava sivu.”
Vähennyslaskutehtävässä on kaikkiaan 20 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä. Lopuksi lapsen saama pistemäärä puolitetaan, eli tehtävän maksimipistemäärä on 10.
Yhteenlaskut päässälaskuina –tehtävässä lapsen tulee ratkaista päässälaskumuodossa esitettyjä yhteenlaskuja lukualueella 20–60. Opettaja näyttää tehtävälomaketta ja sanoo: ”Tässä on yhteenlaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Jos haluat, voit kirjoittaa paperille miten ratkaisit tehtävän”. Tämän jälkeen lapsi tekee tehtävän loppuun. Tehtävissä on annettu maksimiaikaraja 6 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Yhteenlaskutehtävässä on kaikkiaan 4 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Vähennyslaskut päässälaskuina –tehtävässä lapsen tulee ratkaista päässälaskumuodossa esitettyjä vähennyslaskuja lukualueella 20–60. Opettaja näyttää tehtävälomaketta ja sanoo: ”Tässä on vähennyslaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Jos haluat, voit kirjoittaa paperille miten ratkaisit tehtävän”. Tämän jälkeen lapsi tekee tehtävän loppuun. Tehtävissä on annettu maksimiaikaraja 6 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Vähennyslaskutehtävässä on kaikkiaan 4 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Yhteenlaskut allekkainlaskuina –tehtävässä lapsen tulee ratkaista allekkainlaskumuodossa esitettyjä yhteenlaskuja lukualueella 20–100. Opettaja näyttää tehtävälomaketta ja sanoo: ”Tässä on yhteenlaskuja. Laske lasku ja kirjoita vastaus tehtävään.” Tämän jälkeen lapsi tekee tehtävän loppuun. Tehtävissä on annettu maksimiaikaraja 6 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Tehtävässä on kaikkiaan 4 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Vähennyslaskut allekkain –tehtävässä lapsen tulee ratkaista allekkainlaskumuodossa esitettyjä vähennyslaskuja lukualueella 20–100. Opettaja näyttää tehtävälomaketta ja sanoo: ”Tässä on vähennyslaskuja. Laske lasku ja kirjoita vastaus tehtävään.” Tämän jälkeen lapsi tekee tehtävän loppuun. Tehtävissä on annettu maksimiaikaraja 6 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Tehtävässä on kaikkiaan 4 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Kevään tehtävät
Lukumääräisyyden tajua arvioiva tehtävä
Lukumääräisyyden tajua arvioidaan Lukujen suuruusvertailun ja suuruusjärjestyksen hallinnan tehtävillä.
Lukujen suurusvertailun tehtävässä lapsen tulee valita annetuista luvuista suurin. Keväällä vertaillaan sata- ja tuhatlukuja. Lapsella on edessään tehtäväpaperi, jossa on yhdellä rivillä neljä lukua. Opettaja osoittaa ensimmäisen rivin lukuja (301 299 103 286) ja sanoo: ”Tässä on lukuja. Katso huolellisesti kaikki luvut. Mikä näistä on suurin luku? Rastita oikea vastaus”. Tämän jälkeen oppilas tekee tehtäväsivun loppuun. Suuruusvertailun tehtävässä on kaikkiaan 6 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos rasti puuttui, oli väärän luvun päällä tai rasteja oli osiossa enemmän kuin yksi, annettiin nolla pistettä.
Lukujen suuruusjärjestys –tehtävässä lapsen tulee kirjoittaa annetut luvut suuruusjärjestyksessä. Lukualue on 100–1100. Yhdellä rivillä on neljä lukua (esim. 122 102 112 201) ja lukujen alapuolella neljä tyhjää viivaa. Opettaja osoittaa ensimmäisen rivin lukuja ja sanoo: "Tässä on lukuja. Katso huolellisesti kaikki luvut. Kirjoita luvut suuruusjärjestykseen, pienin ensin." Tämän jälkeen oppilas tekee tehtäväsivun loppuun. Tehtävässä on kaikkiaan 3 osiota. Jokaisesta oikeasta vastauksesta (neljä lukua järjestetty oikein) annettiin yksi piste. Jos yksikin luku puuttui, tai oli väärässä kohdassa, annettiin nolla pistettä.
Aritmeettisia perustaitoja arvioivat tehtävät
Aritmeettisten perustaitojen ryppäästä arvioidaan yhteen- ja vähennyslaskun sujuvuutta lukualueella 1–20 sekä päässä- ja allekkainlaskua lukualueella 20–100.
Yhteenlaskun sujuvuus –tehtävässä lapsen tulee ratkaista niin monta laskua kuin mahdollista yhden minuutin aikana. Lukualue on 1–20. Ohjeistuksen aikana lapsen tulee pysyä STOP–merkillä kuvitetulla odota-sivulla. Opettaja näyttää tehtävälomakkeesta laskutehtävää ja sanoo: ”Seuraavaksi näet yhteenlaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Laske laskut ylhäältä alas. Aloita harmaasta sarakkeesta ja jatka sitten valkoiseen. Laske tehtäviä niin pitkälle kuin ehdit.”
”Kun annan luvan, voit kääntää sivua ja aloittaa tehtävän. Heti, kun sanon SEIS, lopeta tehtävä ja laita kynä pöydälle. Laske mahdollisimman nopeasti ja tarkasti. No niin, ota kynä käteen ja käännä sivua. ALOITA.” Kun yksi minuutti on kulunut opettaja sanoo: ”SEIS. Hyvä, laita kynä pöydälle ja käännä seuraava sivu.”
Yhteenlaskutehtävässä on kaikkiaan 20 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä. Lopuksi lapsen saama pistemäärä puolitetaan, eli tehtävän maksimipistemäärä on 10.
Vähennyslaskun sujuvuus –tehtävä on ohjeistukseltaan yhteenlaskutehtävän kanssa identtinen. Lapsen tulee ratkaista niin monta laskua kuin mahdollista yhden minuutin aikana. Lukualue on 1–20. Ohjeistuksen aikana lapsen tulee pysyä STOP–merkillä kuvitetulla odota-sivulla. Opettaja näyttää tehtävälomakkeesta laskutehtävää ja sanoo: ”Seuraavaksi näet vähennyslaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Laske laskut ylhäältä alas. Aloita harmaasta sarakkeesta ja jatka sitten valkoiseen. Laske tehtäviä niin pitkälle kuin ehdit.”
”Kun annan luvan, voit kääntää sivua ja aloittaa tehtävän. Heti, kun sanon SEIS, lopeta tehtävä ja laita kynä pöydälle. Laske mahdollisimman nopeasti ja tarkasti. No niin, ota kynä käteen ja käännä sivua. ALOITA.” Kun yksi minuutti on kulunut opettaja sanoo: ”SEIS. Hyvä, laita kynä pöydälle ja käännä seuraava sivu.”
Vähennyslaskutehtävässä on kaikkiaan 20 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä. Lopuksi lapsen saama pistemäärä puolitetaan, eli tehtävän maksimipistemäärä on 10.
Yhteenlaskut päässälaskuina –tehtävässä lapsen tulee ratkaista päässälaskumuodossa esitettyjä yhteenlaskuja lukualueella 20–100. Opettaja näyttää tehtävälomaketta ja sanoo: ”Tässä on yhteenlaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Jos haluat, voit kirjoittaa paperille miten ratkaisit tehtävän”. Tämän jälkeen lapsi tekee tehtävän loppuun. Tehtävissä on annettu maksimiaikaraja 6 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Yhteenlaskutehtävässä on kaikkiaan 4 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Vähennyslaskut päässälaskuina –tehtävässä lapsen tulee ratkaista päässälaskumuodossa esitettyjä vähennyslaskuja lukualueella 20–100. Opettaja näyttää tehtävälomaketta ja sanoo: ”Tässä on vähennyslaskuja. Laske lasku ja kirjoita vastaus tyhjään ruutuun. Jos haluat, voit kirjoittaa paperille miten ratkaisit tehtävän”. Tämän jälkeen lapsi tekee tehtävän loppuun. Tehtävissä on annettu maksimiaikaraja 6 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Vähennyslaskutehtävässä on kaikkiaan 4 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Yhteenlaskut allekkainlaskuina –tehtävässä lapsen tulee ratkaista allekkainlaskumuodossa esitettyjä yhteenlaskuja lukualueella 20–100. Opettaja näyttää tehtävälomaketta ja sanoo: ”Tässä on yhteenlaskuja. Laske lasku ja kirjoita vastaus tehtävään.” Tämän jälkeen lapsi tekee tehtävän loppuun. Tehtävissä on annettu maksimiaikaraja 6 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Tehtävässä on kaikkiaan 4 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Vähennyslaskut allekkain –tehtävässä lapsen tulee ratkaista allekkainlaskumuodossa esitettyjä vähennyslaskuja lukualueella 20–100. Opettaja näyttää tehtävälomaketta ja sanoo: ”Tässä on vähennyslaskuja. Laske lasku ja kirjoita vastaus tehtävään.” Tämän jälkeen lapsi tekee tehtävän loppuun. Tehtävissä on annettu maksimiaikaraja 6 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Tehtävässä on kaikkiaan 4 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Lukujärjestelmätiedon soveltamista laskemisessa arvioiva tehtävä
Lukujärjestelmä tiedon soveltamista laskemisessa arvioidaan yhteen- ja vähennyslaskun täydentämisen tehtävillä.
Yhteenlaskun täydentämisen tehtävässä lapsen tulee täydentää puuttuva yhteenlaskettava. Tehtävän lukualue on 80–1000. Tehtävässä on yhteenlaskulausekkeita, joista puuttuu toinen yhteenlaskettavista. Opettaja näyttää tehtävälomakkeesta ensimmäistä ruutua ja sanoo: ”Tässä tehtävässä on yhteenlaskuja. Täydennä puuttuva luku. Nyt voit täydentää kaikki yhteenlaskut. Laita kynä pöydälle, kun olet valmis." Tehtävissä on annettu maksimiaikaraja 5 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Tehtävässä on kaikkiaan 5 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Vähennyslaskun täydentämisen tehtävässä lapsen tulee täydentää puuttuva vähenevä tai vähentäjä. Tehtävän lukualue on 80–1000. Tehtävässä on vähennyslaskulausekkeita, joista puuttuu toinen tekijä. Opettaja näyttää tehtävälomakkeesta ensimmäistä kohtaa ja sanoo: ”Tässä tehtävässä on vähennyslaskuja. Täydennä puuttuva luku. Nyt voit täydentää kaikki vähennyslaskut. Laita kynä pöydälle, kun olet valmis." Tehtävissä on annettu maksimiaikaraja 5 minuuttia, jonka jälkeen tehtävä lopetetaan. Jos kaikki ovat valmiita, voit siirtyä seuraavaan tehtävään jo aikaisemmin. Tehtävässä on kaikkiaan 5 osiota. Jokaisesta oikeasta vastauksesta annettiin yksi piste. Jos vastaus puuttui, oli väärä tai vastauksia oli useita, annettiin nolla pistettä.
Viiteaineiston tulokset
Mittarien rakenne ja luotettavuus
Reliabiliteetti. Tehtävien kykyä mitata luotettavasti tutkimuksen kohteena olleita taitoja arvioitiin laskemalla syksyn, talven ja kevään osioille Cronbachin alfa ja Split half –kertoimet. Vastaavat tarkastelut tehtiin myös syksyn osataidoille. Molempien kertoimien arvo voi vaihdella välillä 0–1. Korkea arvo, joka on lähellä yhtä, kertoo osioiden vahvoista keskinäisistä korrelaatioista ja hyvästä sisäisestä yhtenäisyydestä. Cronbachin alfa –kerroin kertoo arviointivälineen sisäisestä yhtenäisyydestä eli siitä, kuinka hyvin tehtävän osiot mittaavat samaa asiaa. Split half –kerrointa laskettaessa tehtävän osiot jaetaan kahteen puolikkaaseen, jonka jälkeen lasketaan puolikkaiden korrelaatio ja sen avulla lasketaan itse kerroin. Split half -kerrointa laskettaessa on mahdollisuus huomioida osioiden vaikeustaso sijoittamalla eri puolikkaisiin yhtä vaikeita osioita. Eri tehtävien Cronbachin alfa ja Split half –kertoimet on esitetty taulukossa 2. Kokonaissummien Cronbachin alfa –kertoimet olivat erinomaisia ollen kaikissa arviointivälineissä noin 0,94, mikä osoittaa tehtävien olleen osiorakenteiltaan yhtenäisiä. Kokonaissummien Split half –kertoimien arvot, 0,94–0,95, tukivat näkemystä siitä, että mittarit mittaavat kokonaisuudessaan luotettavasti kohteena olleita taitoja. Syksyn osaitaitojen Cronbachin alfa- ja Split half –kertoimet kertoivat hyvästä sisäisestä yhteneväisyydestä ollen pääsääntöisesti yli 0,80. Poikkeuksena oli Rahojen laskemisen tehtävä, jonka sisäinen yhteneväisyys oli hieman muita osatehtäviä heikompi.
| Cronbachin alfa | Split half | |
|---|---|---|
| Syksyn tehtävät | 0,94 | 0,95 |
| Osataidot: | ||
| LMT: Suuruusvertailu |
0,81 | 0,85 |
| MSH: Sarjoittaminen | 0,91 | 0,90 |
| LT: Numerosymbolien hallinta |
0,85 | 0,84 |
| APT: Yhteenlaskun sujuvuus |
0,88 | 0,91 |
| APT: Vähennyslaskun sujuvuus |
0,90 | 0,93 |
| LSL: Rahojen laskeminen |
0,67 | 0,70 |
| Talven tehtävät | 0,94 | 0,94 |
| Kevään tehtävät | 0,94 | 0,95 |
Validiteetti. Mittarin on oltava rakenteeltaan luotettava, mutta sen on myös mitattava haluttua taitoa eli oltava validi. Validiteettia voidaan arvioida esimerkiksi vertaamalla tehtävän antaman tuloksen samankaltaisuutta toisen, yleisesti hyväksytyn tai hyväksi tiedetyn tehtävän antamaan tulokseen. Tällaisen rinnakkaisvaliditeetin suoraan arvioimiseen ei tässä ollut mahdollisuutta, koska aineistoa yleisesti hyväksytyillä mittareilla ei ollut saatavilla.
Tehtävätyypit ja tehtävien rakenteet valittiin tutkimustiedon perusteella toisella luokalla kehityksen ja opetuksen keskiössä olevista taidoista (ks. LukiMat-tietopalvelu: Taitojen kehitys). Lähtökohtana oli taitorypäsmalli, jossa matemaattisen osaamisen ajatellaan koostuvan neljästä eri osataidosta: lukumääräisyyden tajusta, matemaattisten suhteiden hallinnasta, laskemisen taidoista ja aritmeettisista perustaidoista. Syksyn osatehtäviksi valittiin tyypillisiä ko. osataitoja mittaavia tehtäviä, jotta voitaisiin päätellä, millä osa-alueella lapsen mahdolliset oppimispulmat tulevat erityisesti esille ja missä hän on vahvoilla. Matemaattisten taitojen kehitys on kuitenkin prosessi, jossa eri osataidot vahvistavat tai kompensoivat toisiaan, eivätkä ne kehity irrallaan toisistaan riippumatta. Toiselle luokalle tultaessa lapsen oletetaankin osaavan peruslaskutoimitukset ja keskeiset matemaattiset käsitteet. Tässä vaiheessa korostuu laskemisen rutinoituminen ja tehokkaampien laskustrategioiden käyttö, minkä vuoksi yhteen- ja vähennyslaskun sujuvuuden tehtävissä onkin aikaraja. Osataitokohtainen tarkastelu tehdään vain syksyllä. Tehtävien kokonaispistemäärä on kuitenkin osataitokohtaisia tarkasteluja ensisijaisempi arvio lapsen taidoista myös syksyllä. Osataitokohtainen tarkastelu toimii lähinnä lisäinformaationa lapsen taitoprofiilin arvioinnissa.
Tehtäväkohtaiset tulokset
Taulukossa 3 on ensin esitetty syksyn koko välinettä koskevat tunnusluvut, sekä osataitokohtaiset tilastolliset tunnusluvut (pistemäärien vaihteluvälit, keskiarvot ja -hajonnat sekä mediaanit ja tyyppiarvot) ja lopuksi talven ja kevään koko välinettä koskevat tunnusluvut.
Mediaani kertoo, mikä on jakauman keskimmäinen arvo. Tyyppiarvo kertoo puolestaan, mikä on jakauman yleisin arvo. Syksyn osatehtävistä yhteenlaskun sujuvuuden ja vähennyslaskun sujuvuuden tehtävät eivät ole vertailukelpoisia muiden tehtävien kanssa, koska niissä on minuutin aikaraja ja maksimipistemäärä on 10. Muissa tehtävissä ei ole aikarajaa tai se on huomattavasti pidempi ja maksimipistemäärä on 8. Näiden tehtävien osalta helpoimpia ovat olleet suuruusvertailun ja numerosymbolien hallinnan tehtävät kun taas sarjoittamisen osatehtävä on ollut hieman vaikeampi, joskin siinäkin tehtävässä tyypillisin pistemäärä on täydet 8 pistettä. Yhteenlaskun sujuvuuden ja vähennyslaskun sujuvuuden tehtävässä harva on saanut vaihteluvälin korkeampia pisteitä. Vähennyslaskut ovat olleet hieman yhteenlaskuja vaikeampia. Syksyn, talven ja kevään kokonaispisteitä ei ole mielekästä vertailla, koska välineiden tehtävämäärä ja vaikeustaso vaihtelevat. Vertailevaa tarkastelua on mahdollista tehdä persentiililukujen avulla.
-
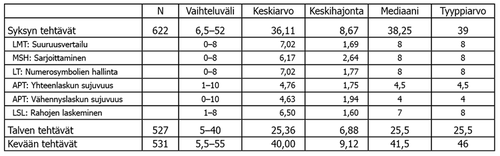
- Taulukko 3. Pistemäärien vaihteluvälit, keskiluvut ja –hajonnat.
Syksyn osataitokohtaiset tulokset
Suuruusvertailutehtävän pistemäärien jakauma 2. luokan syksyllä on esitetty kuviossa 1. Pistemäärien keskiarvo oli 7,02, keskihajonta 1,69 ja vaihteluväli 0–8. Jakaumakuviosta nähdään, että 77,8% vastanneista sai oikein 7 tai 8 tehtävää. Suurin osa lapsista hallitsee suuruusvertailun hyvin syksyllä.
-
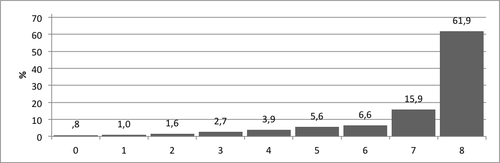
- Kuvio 1. Pistemäärien jakauma Suuruusvertailu–tehtävässä.
Sarjoittamisen osatehtävän pistemäärien jakauma 2. luokan syksyllä on esitetty kuviossa 2. Pistemäärien keskiarvo oli 6,17, keskihajonta 2,64 ja vaihteluväli 0–8. Osataidossa 12,9% saa vain 0 tai 1 vastausta oikein kun taas 66,1% saa oikein 7 tai 8 vastausta. Taidossa on on havaittavissa polarisoitumista ääripäihin, eli sarjoittaminen pääosin joko osataan tai ei.
-
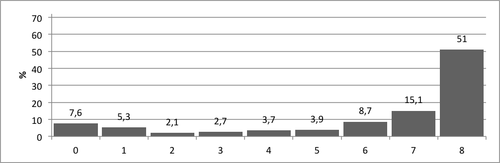
- Kuvio 2. Pistemäärien jakauma Sarjoittaminen–tehtävässä.
Numerosymbolien hallinnan osatehtävän pistemäärien jakauma 2. luokan syksyllä on esitetty kuviossa 3. Pistemäärien keskiarvo oli 7,02 ja keskihajonta 1,77 ja vaihteluväli 0–8. Suurin osa viiteaineistosta (77,3%) sai osatehtävästä 7 tai 8 pistettä kun taas alle prosentti ratkaisi oikein vain 0–1 tehtävää.
-
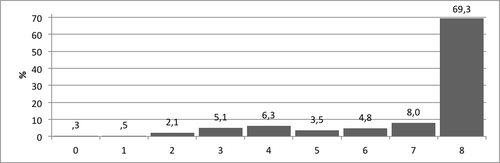
- Kuvio 3. Pistemäärien jakauma Numerosymbolien hallinta -tehtävässä.
Yhteenlaskun sujuvuuden osatehtävän pistemäärien jakauma 2. luokan syksyllä on esitetty kuviossa 4. Tehtävän jakauma on aikarajasta johtuen enemmän normaalinen. Vain harva on saanut tehtävästä täydet tai melkein täydet pisteet. Kuviosta huomataan että 54,3% vastaajista saa tehtävästä 3,5–5 pistettä kun taas erittäin pieniä ja erittäin suuri arvoja saavia on vain vähän. Kaikki vastaajat ovat saaneet tehtävästä vähintään yhden pisteen. Tehtävä erottelee hyvin nopeat ja hitaat laskijat.
-
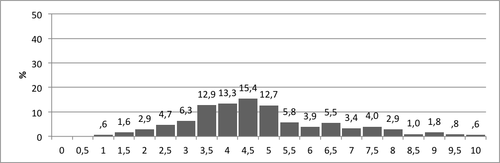
- Kuvio 4. Pistemäärien jakauma Yhteenlaskun sujuvuus -tehtävässä.
Vähennyslaskun sujuvuuden osatehtävän pistemäärien jakauma 2. luokan syksyllä on esitetty kuviossa 5. Tehtävän pisteet painottuvat viiteaineistossa jakauman keskivaiheille 18,5% saadessa tehtävästä neljä pistettä. Tässäkin tehtävässä erottuvat hyvin keskimääräisten laskijoiden lisäksi nopeat ja hitaat laskijat. Toisin kuin muissa tehtävissä, sujuvuuden tehtävissä ei ole samanlaista kattoefektiä (suurin osa saa kaikki oikein) kuin muissa tehtävissä, jotka eivät erottele hyvien laskijoiden välillä vaan paljastavat vain muita selkeästi heikommat.
-
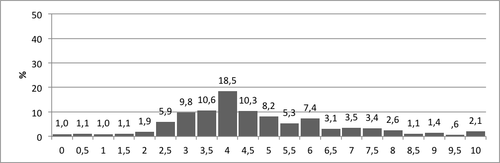
- Kuvio 5. Pistemäärien jakauma Vähennyslaskun sujuvuus -tehtävässä.
Rahojen laskemisen osatehtävän pistemäärien jakauma 2. luokan syksyllä on esitetty kuviossa 6. Tehtävän keskiarvo oli 6,50, keskihajonta 1,60 ja vaihteluväli 1–8. Suurin osa viiteaineiston vastaajista sai tehtävästä 6–8 tehtävää oikein (78,1%). 11,3 % sai viiteaineistossa pisteitä 1–4. Kukaan ei jäänyt viiteaineistossa tehtävässä täysin pisteittä.
-
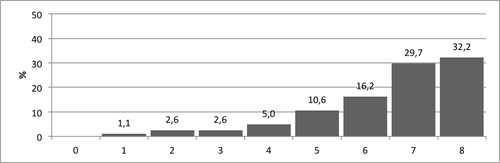
- Kuvio 6. Pistemäärien jakauma Rahojen laskeminen -tehtävässä.
Kokonaissummien jakaumat
Kaikkien ajankohtien kokonaispisteiden jakaumat ovat seuloille tyypilliseen tapaan hieman vasemmalle vinoja. Tämä tarkoittaa sitä, että paljon pisteitä saavia on suhteessa enemmän kuin vähemmän pisteitä saavia. Tehtävät on suunniteltu tunnistamaan ne lapset, joilla on tuen tarvetta ja ne ovatkin suurimmalle osalle lapsista helppoja. Tehtävät eivät siis kykene erottelemaan niitä, jotka suoriutuvat hyvin ja niitä jotka suoriutuvat todella hyvin. Poikkeuksena ovat yhteen- ja vähennyslaskun sujuvuuden tehtävät, jotka aikarajoitteen takia erottelevat hitaiden laskijoiden lisäksi myös erityisen nopeat laskijat. Täten esikoululaisten ja ensimmäisen luokan välineille tyypillinen kattoefekti ei tule yhtä nopeasti vastaan toisen luokan tehtävien summajakaumissa. Vasemmalle vinon jakauman tyyppiarvot ja mediaanit ovat suurempia kuin jakaumien keskiarvot. Jakaumien vinouden vuoksi lasten suoritusten vertailussa ei ole syytä käyttää normaalijakaumaan perustuvia päätelmiä, koska jakauman yläpäässä ei ole riittävästi hajontaa. Normaalijakaumaan suhteuttamisen sijaan lasten suorituksen tulkinta tapahtuu persentiilien eli prosenttipisteiden avulla (ks. persentiilitaulukot). Lapsen kokonaispistemäärää vastaavaa persentiililuku kuvaa sitä, kuinka monta prosenttia viiteaineiston lapsista saa vastaavan tai heikoimman kokonaispistemäärän. Esimerkiksi jos lapsi saa syksyllä yhteensä 39 pistettä, niin sitä vastaava persentiililuku 35 kertoo, että 35% lapsista suoriutuu tehtävissä yhtä hyvin tai heikommin.
-
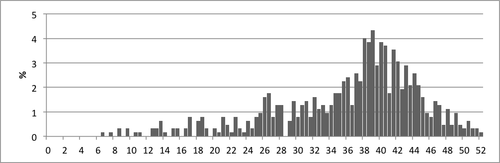
- Kuvio 7. Kokonaispistemäärien jakauma syksyllä.
-
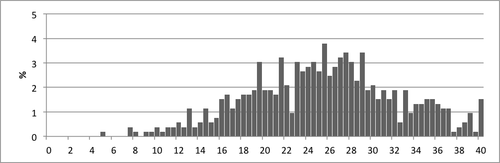
- Kuvio 8. Kokonaispistemäärien jakauma talvella.
-
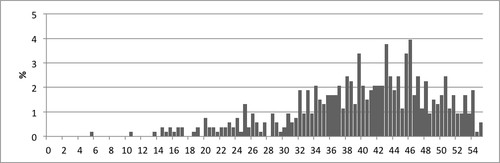
- Kuvio 9. Kokonaispistemäärien jakauma keväällä.
Persentiilitaulukot
Viiteaineiston kokonaispistemäärien perusteella on muodostettu persentiilitaulukko, josta näkyvät ajankohdittain kutakin pistemäärää vastaavat suoritustasot suhteessa viiteaineistoon. Nämä ns. persentiililuvut kertovat kuinka lapsen suoriutuminen tehtävässä sijoittuu suhteessa samalla luokkatasolla oleviin lapsiin. Esimerkiksi persentiililuku 10 kertoo, että lapsen suoritus sijoittuu alimpaan 10%:iin, eli 10 prosenttia viiteryhmän lapsista saa saman tai alhaisemman ja vastaavasti 90 prosenttia paremman pistemäärän tehtävässä. Persentiililukujen käyttö mahdollistaa myös lapsen suoritusten vertailun eri ajankohtien välillä, sillä niiden laskemisessa otetaan huomioon eri ajankohtien tehtävien mahdolliset vaikeustasoerot. Esimerkiksi jos lapsen syksyn kokonaispistemäärä vastaa persentiilitasoa 50 ja kevään kokonaispistemäärä persentiilitasoa 30, voidaan todeta, että ikätasoon nähden lapsen suoriutuminen oli heikompi keväällä kuin syksyllä.
-
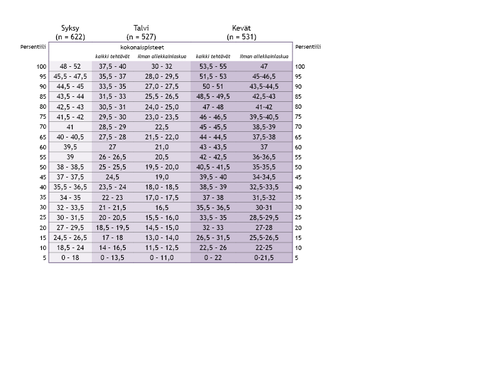
- Taulukko 4. Toisen luokan persentiilitaulukko kokonaispisteistä arviointiajankohdan mukaan.
Tehtävien väliset korrelaatiot syksyllä
Tehtävien väliset korrelaatiot syksyllä on esitetty taulukossa 5. Kertoimet ovat järjestyskorrelaatioita, koska osataitojen jakaumat olivat pääosin vinoja. Huomattavin korrelaatio on yhteenlaskun sujuvuuden ja vähennyslaskun sujuvuuden tehtävien välillä (0,75). Sujuvat laskijat näyttävät siis olevan nopeita riippumatta siitä, kumpi laskutoimitus on laskettavana ja vastaavasti heikot laskijat laskevat hitaasti sekä yhteen- että vähennyslaskuissa. Eksploratiivisessa faktorianalyysissa sujuvuuden tehtävät latautuvat omaksi faktorikseen etenkin pojilla sekä iältään nuoremmilla lapsilla.
-
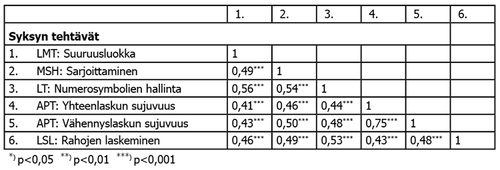
- Taulukko 5. Syksyn tehtävien korrelaatiot.
Iän ja sukupuolen vaikutukset tuloksiin
Iän vaikutusta tehtävissä suoriutumiseen tarkasteltiin korrelaatioilla ja vertaamalla eri ajankohdissa iän mediaanin perusteella jaettuja ryhmiä toisiinsa (syksyllä nuorempien lasten ryhmän ikä oli keskimäärin 7 v 11 kk ja vanhempien lasten ryhmän ikä keskimäärin 8v 5 kk). Korrelaatiotarkasteluissa ei havaittu yhteyksiä iän ja tehtäväpistemäärien välillä. Vertaamalla samanaikaisesti kahden ikäryhmän ja toisaalta tyttöjen ja poikien pistemäärien keskiarvoja toisiinsa, saatiin iän ja sukupuolen omavaikutuksien lisäksi selville myös mahdolliset yhdysvaikutukset eli se, olivatko ikäryhmän vaikutukset keskimääräisiin pistemääriin erilaisia pojilla ja tytöillä. Yhteenvetona voidaan todeta, että poikien keskimääräinen pistemäärä oli tyttöjä suurempi kaikissa arviointiajankohdissa, mutta suurimmillaan kokonaispisteiden erot sukupuolien välillä olivat syksyllä (ero ka. 3,96 pistettä). Pojat saivat keskimäärin enemmän pisteitä kaikissa syksyllä arvioiduissa osataidoissa. Vanhemmat lapset saivat nuorempia lapsia enemmän pisteitä syksyllä (ero ka. 1,82 pistettä) ja talvella (ero ka. 1,27 pistettä), mutta keväällä eroja nuorempien ja vanhempien kesken ei enää ollut. Iän vaikutus kokonaispisteiden keskiarvoon oli samanlainen sekä tytöillä että pojilla, eli iän ja sukupuolen yhdysvaikutuksia ei tullut esiin missään ajankohdassa.
-
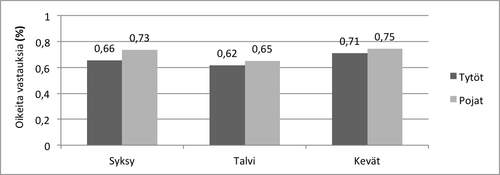
- Kuvio 10. Oikeiden vastausten osuudet sukupuolittain.
