Aritmeettiset perustaidot
Yhteenlasku
Suomalaisissa matematiikan oppikirjoissa opetetaan tällä hetkellä yhteenlaskut (luvuilla 1-9) pääasiassa niin sanottujen hajotelmien kautta. Esimerkiksi lukua kuusi opeteltaessa opetellaan kaikki luvun aritmeettiset yhdistelmät, kuten 0 + 6, 1 + 5, 2 + 4, 3 + 3, 4 + 2, 5 + 1 ja 6 + 0. Yksittäisten laskujen oppiminen on erityisesti taidoiltaan heikolle lapselle haastava, jos hän ei löydä laskuista kiinnekohtia toisiin laskuihin vaan näkee kaikki laskut irrallisina. Laskeminen on hidasta, jos lapsi tukeutuu siinä vain luettelemalla laskemiseen. Viimeaikaiset tutkimukset kehottavat opettamaan erityisesti heikoimmille lapsille laskustrategioita, joita lapsi ei välttämättä itse oivalla. Laskustrategioiden opettamisen kautta pyritään vähentämään ulkoa opittavan tiedon määrää. Niissä esitetään, kuinka tiettyjen muistissa olevien laskujen avulla voidaan ratkaista myös sellaisia laskuja, jotka tuntuvat vaikeasti muistettavilta. Näin pystytään myös luettelemalla laskemisen määrää minimoimaan. Harjoittelussa käytetään konkreettista ja visuaalista materiaalia ja lasta autetaan keskustelemalla löytämään yhteyksiä laskujen välille. Laskuja voidaan vahvistaa muun muassa pelien kautta. Automatisoituneita laskuja pyritään siirtämään suuremmille lukualueille analogioiden kautta (esim. 2 + 3, 20 + 30). Harjoittelussa korostetaan ymmärtämistä mekaanisen luettelemalla laskemisen tai ulkoa oppimisen sijaan.
Seuraavan mallin avulla laskustrategioita voidaan opettaa lapselle, jonka on vaikea muistaa perusyhteenlaskuja lukualueella 0-20. Mallia voidaan soveltaa myös koko opetusryhmään. Malli ja harjoitukset pohjautuvat Suomessa kehitettyyn kuntoutus- ja/tai opetusmenetelmään (Koponen 2007,2008; Koponen & Mononen 2009) sekä seuraavaan kirjallisuuteen: Cotter 2007, Haylock & Cockburn 2008, Koponen, Aro & Ahonen 2009 sekä Wright, Martland, Stafford & Stanger 2006.
Mitä laskuja lapsi jo hallitsee?
Kun lapsen kanssa aletaan harjoitella yhteenlaskutaitoa, on selvitettävä, millaisia laskuja lapsi jo osaa. Tämä voi tapahtua esimerkiksi yhteenlaskukorttien sekä yhteenlaskutaulukon avulla. (Lataa tästä tulostettava taulukko ja kortit, pdf.) Arvioinnin voi toteuttaa pelinomaisesti. Opettaja tai lapsi laittaa yhden laskukortin kerrallaan pöydälle. Jos lapsi pystyy vastaamaan kortissa olevaan laskuun nopeasti (noin 3–4 sekunnin aikana), hän saa kortin itselleen. Ne laskut, joihin lapsi ei pysty vastaamaan nopeasti, laitetaan toiseen pinoon. Taulukosta ympyröidään ne laskut, joihin lapsi osasi vastata nopeasti. Taulukon pohjalta aletaan opettaa ja harjoitella niitä laskuja, joita lapsi ei hallinnut. Keskeistä on löytää laskujen rakenteista säännönmukaisuuksia ja auttaa lasta oivaltamaan, miten tieto lukujonosta ja luvun käsitteestä toimii laskemisen apuna. Toisaalta harjoittelussa opetellaan hyvin tietyt ns. ankkurilaskut (esim. tuplat ja kymppiparit) ja näiden varassa harjoitellaan päättelemään muita laskuja. Laskukorttien avulla voidaan myös jatkossa arvioida, onko lapsi oppinut opiskeltavana olleet laskut. Taulukkoon ympyröidään silloinkin laskut, jotka lapsi hallitsee. Näin myös lapsi oppii tietämäään mitä osaa ja mitä laskuja pitää vielä harjoitella.
-
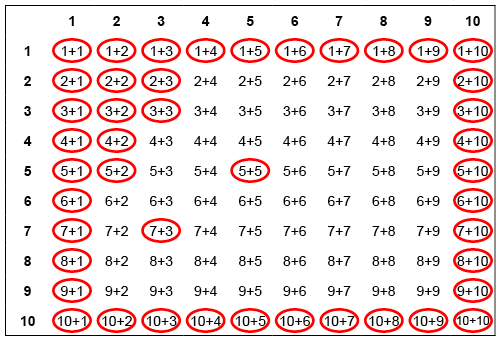
- Esimerkki taulukosta, johon on merkitty lapsen jo hallitsemat yhteenlaskut.
Strategioiden opetusjärjestys
Seuraavassa on esitelty eräs malli opetusjärjestyksestä, jossa on pyritty huomioimaan laskujen oppimisen vaikeusaste sekä laskujen yhteydet toisiinsa. Lapset oppivat laskemista kuitenkin aina hyvin yksilöllisesti. On hyvin mahdollista, että vaikka lapsi osaa yhdenlaiset laskut, hän ei osaa luettelossa aiemmin esitettyjä laskuja. Joidenkin laskujen ratkaisemisessa voidaan käyttää useaa eri strategiaa, joista lapsi voi valita hänelle sopivimman.
|
Laskutyyppi |
Harjoittelu/tausta-ajatus |
|---|---|
| 1) Luku + 1 -laskut | lukukäsite / lukujono+ visuaalinen tuki |
| 2) Luku + 2 -laskut | lukujono / parillinen ja pariton luku käsitteet + visuaalinen tuki |
| 3) Viisi + luku 1–5 -laskut | lukujen 6-10 käsitteet + visuaalinen tuki |
| 4) Kymppiparilaskut | ankkurilaskut |
| 5) Kymppiparien lähilaskut |
kymppiparin avulla päättely |
| 6) 10+ luku -laskut | lukujen 11-20 käsite |
| 7) Laskut luvuilla 5 - 9 | luvut viiden kautta jäsenneltynä |
| 8) Tuplalaskut | ankkurilaskut: lukujono + sääntö + visuaalinen tuki |
| 9) Lähituplalaskut | tuplalaskun avulla päättely |
| 10) 9- ja 8 -laskut | 10-laskun avulla päättely |
| 11) Kaikkien laskujen vahvistaminen | erilaisten pelien ja tehtävien avulla harjoittelu |
Kustakin laskutyypistä annetaan esimerkkiharjoituksia. Keskeistä harjoittelussa on opettajan ja lapsen/lasten välinen vuorovaikutus ja keskustelu. Kysellen ja kuunnellen lapsen ratkaisumalleja ja matemaattista ajattelua opettaja voi johdatella opetusta eteenpäin ja varmistua, että lapsi ymmärtää opetettavan kohdan.
Luku + 1 -laskut
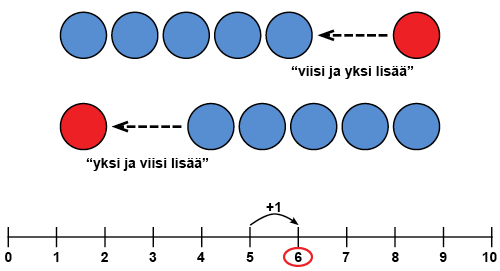
Kun lukuun lisätään yksi, saadaan seuraava luku. Jos lapsi ei tiedä, mitä on 2 + 1 tai 4 + 1, on hyvä tarkistaa, pystyykö hän lukujonossa sanomaan luvusta seuraavan luvun lukualueella 1-10 tai pystyykö hän kertomaan konkreettisessa tilanteessa vastaavan laskun vastauksen (esimerkiksi: "Montako omenaa pussissa on, kun siellä aluksi oli 4 ja 1 laitettiin lisää?"). Jos konkreettiset tilanteet onnistuvat, harjoitellaan aluksi lukujonoa ja vahvistetaan lukukäsitetiedon yhteyttä laskemiseen, siis selkeytetään yhteenlaskun käsitettä.
Havainnollistamisessa voidaan käyttää apuna esimerkiksi laskukiekkoja ja lukusuoraa. Konkreettisen materiaalin avulla voidaan myös havainnollistaa vaihdantalakia; esimerkiksi 5 + 1 = 6 ja 1 + 5 = 6. Lasta voidaan pyytää miettimään, kumpi laskuista on helpompi laskea. Yhdessä konkretisoidaan, kuinka numerot voidaan yhteenlaskussa vaihtaa toisinkinpäin.
Luku + 2 -laskut
Luku + 2 -laskut pohjautuvat hyvin pitkälle lukujonon hallintaan. Jos lapsi pystyy kertomaan, mikä luku tulee kahden askeleen jälkeen annetusta luvusta, tai luettelemaan lukuja kahden askeleen välein, on hänellä työkalu, jolla selvittää luku + 2 -laskut. Tällöin tarvitaan symbolein esitetyn laskun ja lukujonossa liikkumisen yhteyden vahvistusta.
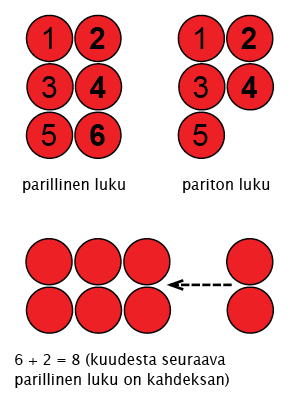
Lukujonossa liikkumisen tueksi voi ottaa parillisen ja parittoman luvun käsitteet. Laskukiekkojen avulla voidaan muodostaa lukuja niin, että kiekot järjestetään allekkain kaksi rinnakkain (ks. kuva). Lapsi voi kuljettaa sormiaan kiekkojen päällä (etu- ja keskisormi yhtä aikaa kahden kiekon päällä) ja tuntea, kuinka parillinen ja pariton luku tuntuvat luettelemisen lopuksi erilaisilta.
Kiekkoja voidaan laskea ensin niin, että kaikki kiekot lasketaan yksitellen painottaen parillista lukua ja lopulta laskien kiekot kaksi kerrallaan. Kun parilliseen lukuun lisätään kaksi, saadaan vastaukseksi aina seuraava parillinen luku. Kun parittomaan lukuun lisätään kaksi, saadaan vastaukseksi seuraava pariton luku.
Lukujonoharjoittelun tueksi voidaan pienten lasten kanssa käyttää Nallelorua (lataa tästä Nalleloru, pdf). Lorussa voidaan painottaa parillisia lukuja. Lukujonoa kymmeneen asti voidaan myös luetella vuorolukuna niin, että toinen ryhmä sanoo parittomat luvut hiljaa ja toinen ryhmä parilliset luvut voimakkaammin. Lopulta voidaan luetella vain parillisia tai parittomia lukuja (esim. 2, 4, 6, 8 jne.). Kun lapsi osaa parilliset ja parittomat luvut, on kahden lisääminen lukuun helpompaa.
Viisi + luku 1–5 -laskut
Luvut 6–10 voidaan opettaa jo alusta alkaen viiden kautta, jolloin myös laskut 5 + luku 1–5 tulevat tutuiksi. Taitoa osittaa luvut 6–10 viiden kautta voidaan käyttää myöhemmin hyväksi, kun yhteenlaskettavat ovat yhtä suuria tai suurempia kuin viisi (ks. tarkemmin kohta Laskut luvuilla 5-9). Laskuja 5 + 1, 5 + 2, 5 + 3, 5 + 4 ja 5 + 5 voidaan havainnollistaa hyvin sormilla tai kaksivärisillä laskukiekoilla. Sormilla lukumääriä näytettäessä lukumäärä 5 on aina vasen käsi ja siihen lisätään tarvittava määrä oikean käden sormia. Lukumääriä 5 + luku 1–5 voidaan aluksi mallintaa sormilla ja pyytää lasta näyttämään ne samalla tavalla. ”Nosta viisi sormea toisesta kädestä; nosta yksi sormi toisesta kädestä; katso sormiasi ja kerro kuinka monta sormea on nostettu?” Pienten lasten kanssa voidaan myös harjoitella lukujen näyttämistä sormista lorun avulla (lataa ja tulosta tästä Nallen kymppiräppi, pdf).
Kymppiparilaskut
Kymppipareilla tarkoitetaan laskuja, joissa yhteenlaskettavien summa on tasan kymmenen (esim. 4 + 6). Kymppiparien hyvä hallinta auttaa lasta esimerkiksi kymppiparien lähilaskuissa (kuten 4 + 5) sekä laskuissa, joissa yhteenlaskettava on 8 tai 9.
Kymppiparien harjoittelu on hyvä aloittaa konkreettisesti jakamalla 10 asiaa eri tavoin kahdelle. Välineinä tehtävässä voi olla esimerkiksi laskukiekkoja. Jakaa voidaan esimerkiksi 10 koirankeksiä kahdelle koiralle sekä 10 karkkia tai 10 euron kolikkoa kahdelle lapselle. Erilaiset jaot voidaan kirjata esimerkiksi piirtämällä ja kirjoittamalla paperille.
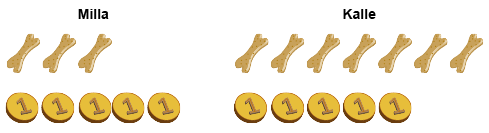
Lopuksi erilaiset yhdistelmät voidaan järjestää niin, että laskujen yhdenmukaisuus tulee näkyviin.
| 0 + 10 |
| 1 + 9 |
| 2 + 8 |
| 3 + 7 |
| 4 + 6 |
| 5 + 5 |
| 6 + 4 |
| 7 + 3 |
| 8 + 2 |
| 9 + 1 |
| 10 + 0 |
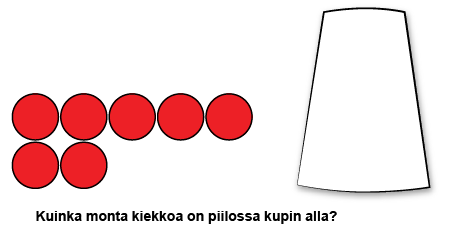
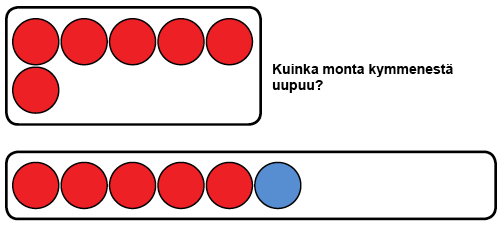
Toiseksi voidaan harjoitella tunnistamaan puuttuva määrä, esimerkiksi paljonko puuttuu kymmenestä. Sitä voidaan tehdä esimerkiksi sormilla, laskukiekoilla tai korttipelin avulla. Sormista voidaan nostaa tietty määrä ylös ja kysyä, kuinka monta on alhaalla (esim. 2 ylhäällä, 8 alhaalla). Jo käytetään laskukiekkoja, osa kymmenestä laskukiekosta voidaan piilottaa purkin tai käden alle, ja sitten lapselta kysytään, kuinka monta kiekkoa on piilossa. Jotta tehtävä kohdistuu juuri kymppiparin harjoitteluun, on kiekot hyvä pitää ryhmiteltyinä viiden ryhmiin. Näin lapsen on nopeampaa hahmottaa näkyvissä oleva määrä. Kiekoista voidaan tehdä myös kortit, joissa on näkyvillä 0–10 kiekkoa ja lapsen pitää sanoa kuinka monta kymmenestä uupuu. Voit ladata ja tulostaa tästä vastaavat lukumääräkortit.
Pelaaminen motivoi usein lapsia toistamaan opeteltavia laskuja, koska jokainen peli on aina erilainen. Kaatispeli on peli kymppipareista 2–4 pelaajalle. Peliä varten tarvitaan pelikorteiksi joko tavallisista pelikorteista kuusi sarjaa kortteja 1–9 (yht. 54 korttia) tai voit myös ladata ja tulostaa tästä pelikortit. Korttipohjat voi tulostaa värilliselle paperille, leikata ja laminoida. Tästä voit ladata ja tulostaa peliohjeet Kaatispeliin. Pelikortteja voidaan käyttää myös muissa tällä sivustolla esiteltävissä korttipeleissä.
Tietokoneavusteisia harjoitteita kymppipareista löytyy mm. Neure-Express-ohjelman yhteenlaskut-osiosta.
Kymppiparien lähilaskut
Kymppiparien lähilaskuiksi sanotaan laskuja, joissa toinen yhteenlaskettavista on yhden suurempi tai pienempi kuin toinen kymppiparilaskun tekijöistä (esim. kymppiparin 7 + 3 lähilaskuja ovat 7 + 4, 4 + 7, 7 + 2 ja 2 + 7). Laskujen ratkaisemisessa voi siis käyttää apuna opittuja kymppipareja. Harjoituksissa rakennetaan ensin kymppipari, johon lisätään tai josta vähennetään yksi, jolloin saadaan opeteltava lasku. On tärkeää, että lapsen kanssa keskustellaan niin pitkään, että hän huomaa kahden laskun yhteyden toisiinsa. Lapsi voi oivaltaa, että lähilaskuissa, joissa toinen tekijä on yhden suurempi, kuin kymppiparilaskun toinen tekijä, vastaus on aina 11. Yhtenä harjoittelutehtävänä lasta voidaankin pyytää keksimään yhteenlaskuja, joissa vastaus on 11.
10 + luku -laskut
Luvut 11–19 muodostuvat kymmenestä sekä ykkösistä. Tietoa siitä, että esimerkiksi 15 on 10 + 5, lapsi voi käyttää hyväkseen esimerkiksi luvun 8 tai 9 sisältävissä laskuissa. Niissä voi ensin miettiä, mikä vastaus olisi jos 8 tai 9 korvattaisiin luvulla 10 (ks. tarkemmin 9- ja 8-laskut) Havainnollistettaessa 10-laskuja, lasta on hyvä muistuttaa myös vaihdantalaista: yhteenlaskettavien laskemisjärjestyksellä ei vastauksen kannalta ole väliä. Lapsi voi kääntää yhteenlaskettavat niin päin, kumpi on järjestyksenä tutumpi.
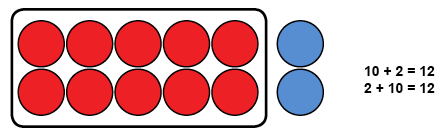
Laskukiekoista kymmentä pidetään koko ajan koskemattomana ja ykkösten määrää vaihdellaan. Lasta voidaan pyytää nimeämään ja/tai kirjoittamaan lasku tai rakentamaan se kirjoitetusta tai sanotusta muodosta. Kymmenen laskukiekkoa voidaan kiinnittää paperille sinitarralla, jolloin niitä voidaan liikutella helposti, kun rakennetaan laskuja tai lisätään kymmenen johonkin lukuun (esim. 3 + 10).
Laskut luvuilla 5-9
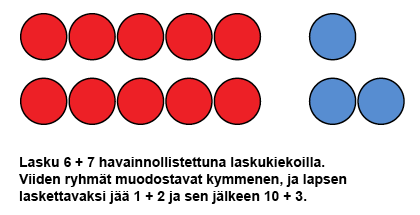
Kun lapsi osaa osittaa luvut 6–10 viiden kautta, voidaan tätä käyttää hyväksi kaikissa laskuissa, joissa yhteenlaskettavat ovat väliltä 5-9. Laskuja voidaan havainnollistaa laskukiekoilla sekä sormilla. Esimerkkilasku on 6 + 7 voidaan havainnollistaa kahdenvärisillä laskukiekoilla viiden ryhmien kautta, kuten alla olevassa kuvassa. Lapsi pystyy havaitsemaan helposti kaksi viiden ryhmää, joista tietää muodostuvan kymmenen. Näin hänelle jää laskettavaksi 1 + 2, jonka hän tietää olevan 3. Kun laskut yhdistetään, saadaan 10 + 3, jonka lapsi on oppinut aiemmin ja tietää olevan 13.
Sormilla havainnollistettaessa lapsi tietää luvun 6 lukuina 5 ja 1. Näin hän nostaa vain yhden sormen pystyyn ja "laittaa muistiinsa" viitosen. Luku 7 on puolestaan luvut 5 ja 2, jolloin lapsi nostaa toisesta kädestä kaksi sormea ja "laittaa muistiinsa viitosen". Molemmat viitoset ovat muistissa ja muodostavat kymmenen. Lapsi laskee 2 ja 1 yhteen, lisää vastauksen kolme muistissa olevaan kymmeneen ja saa vastaukseksi 13.
Tuplalaskut
Tuplalaskuiksi tai tupliksi kutsutaan laskuja, joissa molemmat yhteenlaskettavat ovat samat (esim. 6 + 6). Laskujen vastaus on aina parillinen luku. Aluksi voidaan harjoitella kuntoon pienet tuplat eli ne laskut, joissa summa on kymmenen tai pienempi. Laskujen havainnollistamisessa voidaan käyttää apuna sormia (pienet tuplat), laskukiekkoja ja vaikka peiliä sekä yhdistää laskut ympäristöstä löytyviin tupliin (esim. auton etu- ja takarenkaat 2 + 2 = 4, muurahaisen jalat 3 + 3 = 6, hämähäkin jalat 4 + 4 = 8 jne.). Pieniä tuplia harjoitellessa lasta voidaan pyytää nostamaan toisesta kädestä esimerkiksi kaksi sormea ja toisesta kädestä kaksi sormea ja pyytää kertomaan vastaus. Tehtävä voidaan tehdä ensin niin, että sormet ovat näkyvillä, ja sitten niin, että sormet pidetään pään yläpuolella ”pupunkorvina”. Lukumääriä voidaan tuplata peilinkin avulla. Kun pelin eteen pannaan kolme laskukiekkoa, peili tuplaa määrän, jolloin kiekkoja on 3 ja 3 eli 6. Peiliharjoituksen tueksi voit ladata ja tulostaa tästä Tupla-lorun.
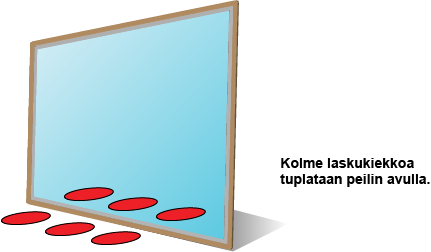
Laskukiekoilla voidaan harjoitella tuplia niin, että opettaja panee ensin pöydälle jonkin määrän kiekkoja ja lapsi tuplaa sen. Kun käytetään kahta väriä, niin lapsen on helpompi havaita kymmenen ryhmä. Kun lapsi on ensin harjoitellut tuplaamista lisäämällä kiekkoja, voidaan kokeilla myös niin, että lapsi vain sanoo vastauksen opettajan rakentamaan tai sanomaan lukuun.
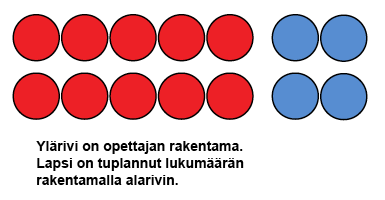
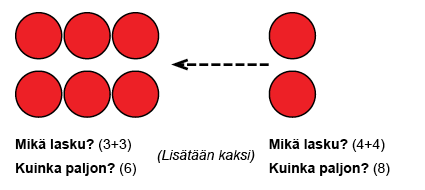
Tuplaamista voidaan harjoitella myös niin, että esillä on vaihtelevasti eri tuolamääriä, joista lapsi keksii laskuja. On tärkeää huomata, että kahden vierekkäisen tuplan välinen ero on aina kaksi.
Tietokoneavusteisia tuplaharjoituksia on mm. Neure-Expressin yhteenlaskut-osiossa.
Lähituplalaskut
Lähitupliksi sanotaan laskuja, joissa yhteenlaskettavat ovat perättäisiä lukuja. Laskujen ratkaisemisessa voi käyttää apuna aiemmin opittuja tuplalaskuja. Harjoituksissa rakennetaan ensin tuplalasku, johon sitten lisätään tai josta vähennetään yksi, jolloin saadaan opeteltava lasku. On tärkeää keskustella lapsen kanssa niin pitkään, että hän oivaltaa kahden laskun yhteyden toisiinsa. Lähituplalaskuissa lapsi voi käyttää apulaskuna pienemmästä yhteenlaskettavasta muodostettavaa tuplalaskua (esim. lasku 5 + 6 voidaan ratkaista laskun 5 + 5 avulla) ja lisätä tuplalaskun vastaukseen yhden. Lasku 5 + 6 voidaan ratkaista myös laskun 6 + 6 avulla, mutta tällöin tuloksesta pitää vähentää yksi. Laskukiekkojen lisäksi pienten tuplien lähituplalaskuja voidaan harjoitella myös sormista. Lapsi laittaa sormet pään yläpuolelle ”pupunkorviksi”. Opettaja sanoo: ”Näytä sormilla kaksi ja kaksi. Kuinka paljon ne ovat yhteensä? Nosta yksi sormi lisää toisesta kädestä. Mitkä luvut sinulla on nyt? Kuinka paljon ne ovat yhteensä?”
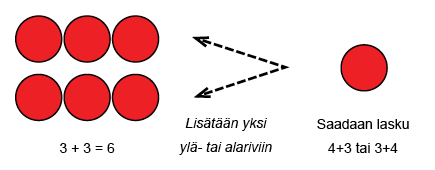
Haastavinta lapselle on oppia, mitä osaamaansa laskua hänen kannattaa käyttää apunaan ratkoessaan sellaisia laskuja, jotka eivät ole vielä automatisoituneet. Apulaskun valinnassa voidaan käyttää harjoitusta, jossa lapsen tulee tehtävän ratkaisemisen jälkeen miettiä, muistiko laskun ulkoa ja mitä apulaskua käytti tarvittaessa. Alla olevassa kuvassa on esimerkki paperilla olevasta harjoituksesta.

(Koponen 2008)
9- ja 8 -laskut
Laskuja, joissa yhteenlaskettavana on 9 tai 8, voidaan pohjata vahvasti kymmenlaskuihin (esim. 10 + 3) sekä hyödyntää laskemisessa jo aiemmin opittuja kymppipareja (esim. 8 + 2). Laskuja voidaan lähestyä kahdella tapaa.
Ensimmäisessä tavassa voidaan ottaa esille kaksi laskua, joita verrataan. Esimerkiksi miten 10 + 5 eroaa laskusta 9 + 5? Asia havainnollistetaan esimerkiksi laskukiekoilla. Koska yhdeksän on yhden pienempi kuin kymmenen, voidaan lasku ajatella ensin kymmenlaskuna ja vähentää summasta yksi (9 + 5 = 10 + 5 – 1). Laskussa 8 + 7, kahdeksan on kaksi pienempi kuin kymmenen, joten kymmenlaskun kautta ajateltuna summasta täytyy vähentää kaksi (esim. 8 + 7 = 10 + 7 – 2).
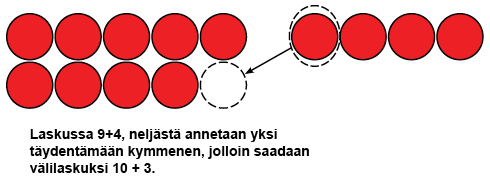
Toinen tapa ajatella 9- ja 8-laskuja on kymmeneen täydentäminen. Aluksi tarkastellaan mikä on luvun 9 ja 10 välinen ero (1). Esimerkiksi laskussa 9 + 4 neljästä annetaan yksi yhdeksälle, jotta se täydentyy kymmeneksi. Välilaskuksi saadaan siten 10 + 3, jonka lapsi on jo oppinut aiemmin. Laskuissa, joissa toinen yhteenlaskettava on 8, huomataan, että kymmenen täyttämiseksi täytyy toisesta yhteenlaskettavasta antaa kaksi pois.
Kaikkien laskujen vahvistaminen
Opittuja laskuja voidaan vahvistaa korttipelien avulla. Jokaisen pelin laskut ovat erilaisia, mikä motivoi lasta pelaamaan pelejä yhä uudelleen. Yhteenlaskusota-peli on kahdelle pelaajalle. Pelistä on kaksi versiota: toisessa lukualue on 1–10 ja toisessa 1–20. Tästä voit ladata ja tulostaa peliohjeen. Pelikorteiksi käyvät tavallisista pelikorteista kortit 1–9, (yht. 36 kpl) tai voit ladata ja tulostaa tästä pelikortit. Korttipohjat voi tulostaa värilliselle paperille, leikata ja laminoida.
Vähennyslasku
Suomalaisissa matematiikan oppikirjoissa opetetaan vähennyslaskua melko rinta rinnan yhteenlaskun kanssa. Joissakin materiaaleissa opetetaan niin sanottujen hajotelmien kautta yhteenlaskujen lisäksi myös vähennyslaskut. Esimerkiksi lukua kuusi opeteltaessa opetellaan kaikki luvun aritmeettiset yhdistelmät, kuten 0 + 6, 1 + 5, 2 + 4, 3 + 3, 4 + 2, 5 + 1 ja 6 + 0, mutta lisäksi voidaan myös opetella laskut 6 – 0, 6 – 1, 6 – 2, 6 – 3, 6 – 4, 6 - 5 ja 6 - 6. On tärkeää, että lapsi huomaa yhtäläisyyden kahden osan ja kokonaisuuden välillä (esim. luvuista 1, 4 ja 5 saadaan neljä erilaista laskua: 1 + 4 = 5, 4 + 1 = 5, 5 - 1 = 4 ja 5 – 4 = 1). Yhteenlaskujen osaaminen voi helpottaa vähennyslaskujen oppimista, kun niiden yhteys tuodaan lapselle esille.
Lukualueella 0 – 20 voidaan tehdä paljon erilaisia vähennyslaskuja. Laskeminen on hidasta, jos lapsi tukeutuu siinä vain luettelemalla laskemiseen. Viimeaikaiset tutkimukset kehottavat opettamaan erityisesti heikoimmille lapsille laskustrategioita, joita lapsi ei välttämättä itse oivalla. Laskustrategioiden kautta pyritään vähentämään ulkoa opittavan tiedon määrää ja osoittamaan lapselle, että tiettyjen muistissa olevien laskujen avulla voidaan ratkaista myös sellaisia laskuja, jotka tuntuvat vaikeasti muistettavilta. Näin pystytään myös luettelemalla laskemisen määrää minimoimaan. Harjoittelussa käytetään konkreettista ja visuaalista materiaalia, autetaan lasta näkemään eri laskujen yhteyksiä sekä vahvistetaan laskuja muun muassa pelaamalla. Automatisoituneita laskuja pyritään siirtämään suuremmille lukualueille analogioiden kautta (esim. 5 - 4, 50 - 40). Harjoittelussa korostetaan ymmärtämistä mekaanisen luettelemalla laskemisen tai ulkoaoppimisen sijaan.
Seuraavassa esitetään malli siitä, kuinka laskustrategioiden opettaminen voisi edetä lapsella, jonka on vaikea muistaa perusvähennyslaskuja lukualueella 0- 20. Mallia voidaan soveltaa myös koko opetusryhmässä käytettäväksi. Malli ja harjoitukset pohjautuvat Suomessa kehitettyyn kuntoutus- ja/tai opetusmenetelmään (Koponen 2007,2008; Koponen & Mononen 2009) sekä seuraavaan kirjallisuuteen: Cotter 2007, Haylock & Cockburn 2008, Koponen, Aro & Ahonen 2009 sekä Wright, Martland, Stafford & Stanger 2006.
Mitä laskuja lapsi jo hallitsee?
Kun lapsen kanssa aletaan harjoitella vähennyslaskuja, on tärkeää arvioida, millaisia laskuja lapsi jo osaa. Tämä voi tapahtua esimerkiksi vähennyslaskukorttien sekä vähennyslaskutaulukon avulla. (Lataa tästä tulostettava taulukko ja kortit, pdf.) Arvioinnin voi tehdä pelinomaisesti. Opettaja tai lapsi laittaa pöydälle yhden kortin kerrallaan. Jos lapsi pystyy vastaamaan laskuun nopeasti (noin 3–4 sekunnin aikana), hän saa kortin itselleen. Ne laskut, joihin lapsi ei pysty vastaamaan nopeasti, laitetaan toiseen pinoon. Taulukosta ympyröidään ne laskut, joihin lapsi osasi vastata nopeasti. Taulukon pohjalta aletaan opettaa ja harjoitella niitä laskuja, joita lapsi ei hallinnut. Keskeistä on löytää laskujen rakenteista säännönmukaisuuksia ja auttaa lasta oivaltamaan, miten yhteenlaskutaito sekä tieto lukujonosta ja luvun käsitteestä toimivat laskemisen apuna. Laskukorttien avulla voidaan myös jatkossa arvioida, onko lapsi oppinut uudet laskut. Taulukkoon ympyröidään silloinkin laskut, jotka lapsi hallitsee. Näin myös lapsi oppii tietämään, mitä osaa ja mitä laskuja pitää vielä harjoitella.
-

- Esimerkki taulukosta, johon on merkitty lapsen hallitsemat vähennyslaskut.
Yhteen- ja vähennyslaskun yhteyden ymmärtäminen
Jos lapsi tajuaa yhteen- ja vähennyslaskujen yhteyden, opittavien laskujen määrä vähenee. Kun lapsi oppii luomaan kytkökset kolmen luvun - kahden osan ja yhden kokonaisen - välille, hän voi tehdä kolmella luvulla neljä erilaista laskua. Yhteyttä voidaan havainnollistaa osat-kokonainen- ympyräkuvion avulla missä tahansa vaiheessa yhteen- ja vähennyslaskuja opeteltaessa. Osat-kokonainen ympyräkuviota voidaan käyttää hyväksi myös yksivaiheisia sanallisia tehtäviä ratkottaessa. Tällöin lapsi asettaa tehtävässä käytetyt luvut oikeisiin ympyröihin ja päättelee sen perusteella, mitä laskutoimitusta tulee käyttää. Osat-kokonainen –ympyräkuvion käyttö soveltuu myöhemmin myös kerto- ja jakolaskuihin. Esikouluvaiheessa, ennen numeroiden kirjoittamista ympyröissä voidaan käyttää esimerkiksi esineitä (tikkuja, laskukiekkoja tms.).


Sellaisissa vähennyslaskuissa, joissa laskun vähennettävä ja vähentäjä ovat lähellä toisiaan, voi käyttää strategiana myös lisäämistä. Laskeminen voi tapahtua lukuja luettelemalla yksitellen vähentäjästä vähennettävään (esim. 8 – 6 voidaan ajatella 6…7, 8). Lapsi voi myös käyttää tukikohtina lukuja 5 ja 10. Jos vähentäjä on pienempi kuin viisi (esim. 7 – 4), sitä voidaan täydentää ensin viiteen (1), jonka jälkeen lisätään tarpeellinen luku, jolla päästään vähennettävään lukuun (7). Lisätyt luvut eli 1 ja 2 lasketaan yhteen, jolloin saadaan vastaukseksi 3. Viiteen täydentämisestä on etua, jos lapsi on oppinut luvut 6–10 viiden kautta (esim. seitsemän on viisi ja kaksi). Kun vähennettävä on suurempi kuin kymmenen, voidaan vähentäjä täydentää ensin kymmeneen ja lisätä sitten vähennettävän ykköset lukuun. Esimerkiksi laskussa 13 – 8 voidaan ensin täydentää kahdeksan kymmeneksi lisäämällä kaksi. Kun lapsi tietää, että 13 on 10 ja 3, lisää hän kymmenestä ylimenevät kolme kahteen ja saa vastaukseksi viisi.

Strategioiden opetusjärjestys
Seuraavassa on esitelty yksi mahdollinen opetusjärjestys, jossa on pyritty huomioimaan laskujen oppimisen vaikeusaste sekä laskujen yhteydet toisiinsa. Lapset oppivat taitoja kuitenkin yleensä eri tahtiin. On hyvin mahdollista, että vaikka lapsi osaa yhdenlaiset laskut, hän ei osaa luettelossa aiemmin esitettyjä laskuja. Joidenkin laskujen ratkaisemisessa voidaan käyttää useaa eri strategiaa, joista lapsi voi valita hänelle sopivimman.
| Laskutyyppi | Harjoittelu/tausta-ajatus |
|---|---|
| 1) Kahden saman luvun vähentäminen toisistaan | lukukäsite/vähennyslaskun käsite |
| 2) Vähennä yksi -laskut | lukukäsite/lukujono+ visuaalinen tuki |
| 3) Vähennä kaksi -laskut | lukujono/parillinen ja pariton luku käsitteet +visuaalinen tuki |
| 4) Perättäisten lukujen vähentäminen toisistaan | lukukäsite/lukujono+visuaalinen tuki |
| 5) Kymmenestä vähentäminen | kymppiparin avulla päättely |
| 6) Luvuista 9 ja 11 vähentäminen | kymppiparin ja 10-x laskun avulla päättely |
| 7) Kymmenen vähentäminen luvusta | lukujen 11-20 käsite |
| 8) Lukujen 8 ja 9 vähentäminen kymmenlaskun kautta | 10-x laskun avulla päättely |
| 9) Tuplat ja lähituplat | yhteen- ja vähennyslaskun välinen yhteys |
| 10) Kaikkien laskujen vahvistaminen | erilaisten pelien ja tehtävien avulla harjoittelu |
Kustakin kohdasta annetaan esimerkkiharjoituksia. Keskeistä harjoittelussa on opettajan ja lapsen/lasten välinen vuorovaikutus ja keskustelu. Kysellen ja kuunnellen lapsen ratkaisumalleja ja matemaattista ajattelua opettaja voi johdatella opetusta eteenpäin ja varmistua, että lapsi ymmärtää opetettavan kohdan.
Kahden saman luvun vähentäminen toisistaan
Kun kaksi samaa lukua vähennetään toisistaan, on erotus aina nolla. Tätä voidaan havainnollistaa antamalla lapselle laskettavaksi sormien tai laskukiekkojen avulla muutamia laskuja (kuten 5 – 5, 3 – 3, 6 – 6) ja kysyä lapselta, huomaako hän laskuissa jotakin sääntöä. Laskut kannattaa kirjoittaa näkyville. Tämän jälkeen voidaan kokeilla samaa vielä muutamalla suuremmalla luvulla (kuten 12 – 12 tai 20 – 20).
Vähennä yksi -laskut
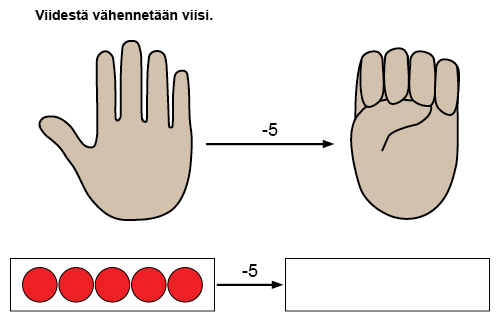
Kun luvusta vähennetään yksi, saadaan vastaukseksi edellinen luku. Asiaa voidaan havainnollistaa esimerkiksi laskukiekoilla ja lukusuoralla ja kysymällä edellistä lukua lukujonosta (esim. mikä luku tulee ennen lukua viisi?).
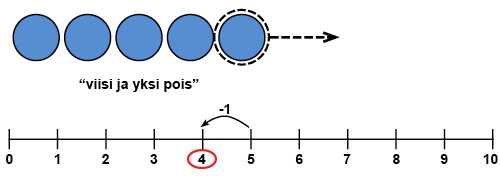
Vähennä kaksi -laskut
Kun lapsi on harjoitellut yhteenlaskuharjoitteissa parillisia ja parittomia lukuja sekä lukujonossa liikkumista kahden välein, voidaan kahden vähentäminen liittää aiemmin opittuun. Kun parillisesta luvusta vähentää kaksi, saa vastaukseksi edellisen parillisen luvun. Kun parittomasta luvusta vähentää parittoman luvun, saa vastaukseksi edellisen parittoman luvun. Laskukiekkojen avulla voidaan muodostaa lukuja niin, että kiekot järjestetään kaksi rinnakkain (ks. kuva). Kiekkoja vähennetään aina kaksi kerrallaan.
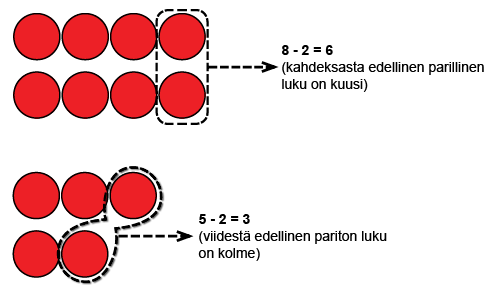
Perättäisten lukujen vähentäminen toisistaan
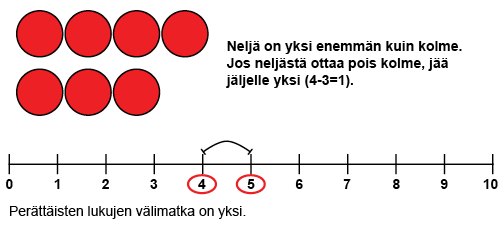
Kun kaksi perättäistä lukua (esim. 4 ja 3) vähennetään toisistaan niin, että suuremmasta vähennetään pienempi, on vastaus aina yksi. Perättäisten lukujen suhdetta toisiinsa voidaan tutkia esimerkiksi laskukiekkojen ja lukusuoran avulla. Laskukiekoilla asiaa tarkastellaan asettamalla pöydälle kaksi perättäistä lukumäärää allekkain. Huomataan, että suuremmassa lukumäärässä on yksi kiekko enemmän. Jos siitä pitäisi ottaa pienemmän luvun verran kiekkoja pois, jäljelle jäisi yksi kiekko. Lukusuoralla asiaa voidaan tarkastella etsimällä kaksi mitä tahansa perättäistä lukua ja katsomalla kuinka paljon niiden etäisyys on toisistaan.
Kymmenestä vähentäminen
Harjoitellessaan kymppipareja yhteenlaskuvaiheessa lapsi oppi tuntemaan laskun puuttuvan tekijän. Tehtävissä harjoiteltiin, kuinka paljon luvusta kymmenen uupuu, tai pääteltiin, kuinka paljon purkin alla oli laskukiekkoja piilossa. Korttipeli 10-pareista harjoitutti myös samaa asiaa. Vähennyslaskuna kymppiparit esitettäisiin esimerkiksi laskuna 10 – 6. Jos lapsi osaa jo kymppiparit, voidaan yhteys vähennyslaskuun esittää esimerkiksi osat-kokonainen –ympyräkuvion avulla. Jos kymppiparit eivät ole automatisoituneet, niitä on syytä harjoitella vielä uudestaan yhteenlaskuissa (ks. tarkemmin tästä).

Luvuista 9 ja 11 vähentäminen
Kun lapsi osaa sujuvasti vähentää kymmenestä, voidaan taitoa käyttää hyödyksi myös vähennettäessä luvuista 9 tai 11 jokin luku. Esimerkiksi laskussa 9 – 6, voidaan ajatella, että ensin vähennetään kymmenestä kuusi, jolloin jää jäljelle neljä. Koska yhdeksän on yhden pienempi kuin luku kymmenen, täytyy vastauksesta vähentää vielä yksi (9 – 6 = 10 – 6 – 1 = 3). Yksitoista puolestaan on yhden suurempi kuin luku kymmenen. Jos lasku ajatellaan ensin kymmenen kautta, tulee vastaukseen lisätä yksi, sillä yksitoista on yhden suurempi kuin kymmenen (esim. 11 – 7 = 10 – 7 + 1 = 4).
Se, että joissakin laskuissa voi käyttää eri strategioita, huomataan esimerkiksi laskussa 9 – 5 tai 9 – 4. Lapsi voi ajatella laskun kymmenen kautta kuten edellä, mutta voi käyttää hyväksi myös tietoa, jolla luku yhdeksän opittiin viiden kautta. Jos lapsi on oppinut, että ”yhdeksän on viisi ja neljä”, voi hän soveltaa tietoa myös kyseisiin vähennyslaskuihin. Sormista katsottuna lasku havainnollistuu myös selvästi.
Kymmenen vähentäminen luvusta
Lapsi on oppinut, että luvut 11–19 muodostuvat kymmenestä sekä ykkösistä. Yhteenlaskuja harjoiteltaessa näistä myös muodostettiin yhteenlaskuja (esim. 10 + 5). Vähennettäessä kymmenen luvuista 11–19, voidaan käyttää lapsen jo oppimaa hyväksi. Asiaa voidaan havainnollistaa osat-kokonainen –ympyräkuvion avulla, jossa lasku voidaan ajatella lisäämisen kautta (kuinka paljon täytyy lisätä tiedettyyn osaan, jotta saadaan kokonainen).
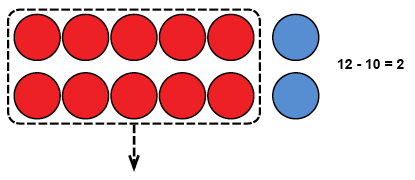
Myös laskukiekot sopivat laskujen havainnollistamiseen. Paperiin on hyvä kiinnittää sinitarralla valmiiksi 10 laskukiekkoa, jolloin niiden siirtäminen on helppoa. Kun luvusta vähennetään kymmenen, jää jäljelle aina ykköset.
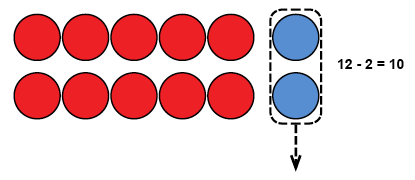
Samalla tavalla voidaan harjoitella myös ykkösten vähentämistä kaksinumeroisesta luvusta lukualueella 11–19. Esimerkiksi laskussa 12 – 2, siirretään pois kaksi laskukiekkoa. Toistettaessa samantyyppisiä laskuja huomataan, että jäljelle jää aina kymmenen, koska luvut 11–19 koostuvat yhdestä kymmenestä ja tietystä määrästä ykkösiä.
Lukujen 8 ja 9 vähentäminen kymmenlaskun kautta
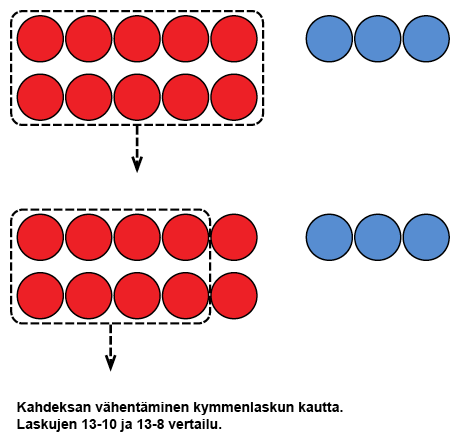
Kun luvusta vähennetään 8 tai 9, voidaan apulaskuna käyttää kymmenlaskua. Kun lapsi hallitsee luvuista 11–19 kymmenen vähentämisen (esim. 16 – 10), voidaan taitoa käyttää hyväksi. Esimerkiksi lasku 13 – 9 voidaan ajatella ensin laskuna 13 – 10, josta saadaan tulokseksi 3. Lapsen kanssa keskustellen ja laskuja 13 – 10 ja 13 – 9 vertaamalla huomataan, että 9 on yhden vähemmän kuin kymmenen, joten vastaukseen tulee näin ollen lisätä vielä yksi. Samoin voidaan toimia kun vähentäjänä on 8. Tällöin verrataan esimerkiksi laskuja 13 – 10 ja 13 – 8, ja huomataan kahdeksan ja kymmenen eroksi kaksi, mikä pitää lisätä laskun vastaukseen, kun lasketaan ensin apulasku 13 – 10 (13 – 8 = 13 – 10 + 2 = 5).
Tuplat ja lähituplat
Tuplien ja lähituplien yhteenlaskun osaamista voidaan hyödyntää myös vähennyslaskuissa. Yhteen- ja vähennyslaskun yhteyttä voidaan jälleen osoittaa osat-kokonainen-ympyräkuviolla. Aluksi ympyräkuvioon voidaan kirjoittaa vain tuplalaskun osat, joista lapsi laskee kokonaisen. Tämän jälkeen voidaan kysyä minkä vähennyslaskun lapsi saa luvuista.
Toiseen osat-kokonainen –ympyräkuvioon voidaan kirjoittaa laskusta lähituplalasku. Jos lapsi osaa esimerkiksi laskun 12 – 6, hän voi käyttää tietoaan hyväksi laskussa 13 – 6, jossa vastaus on tuplalaskua yhden enemmän, koska vähennettäväkin on yhden suurempi. Tarvittaessa tuplien ”puolittamista" voidaan havainnollistaa laskukiekkojen avulla. Aluksi rakennetaan esimerkiksi luvun 6 tuplalasku: ”6 ja 6 on 12”. Sama lasku näytetään vielä osat-kokonainen–ympyräkuviolla. Sitten toinen rivi peitetään: ”12:sta pois 6 on 6”. Sekin näytetään myös ympyräkuviolla.
Kaikkien laskujen vahvistaminen
Opittuja laskuja voidaan vahvistaa pelien avulla. Jokaisen pelin laskut ovat erilaisia, mikä motivoi lasta pelaamaan pelejä yhä uudelleen. Vähennyslaskusota-peli on kahdelle pelaajalle. Pelistä on kaksi versiota: toisessa lukualue on 0–10 ja toisessa 0–20. Voit ladata ja tulostaa tästä peliohjeen. Pelikorteiksi käyvät tavallisista pelikorteista kortit 1 – 10, (yht. 40 korttia). vaihtoehtoisesti voit ladata ja tulostaa pelikortit tästä. Korttipohjat voi tulostaa värilliselle paperille, leikata ja laminoida.



