Matemaattisten suhteiden ymmärtäminen
Hyvän peruslaskutaitopohjan lisäksi toinen hyvin keskeinen taitokokonaisuus alkuopetusikäisten lasten matematiikassa on lukujärjestelmän hallinta. Jotta lapsi pystyy ymmärtämään ja tuottamaan lukuja sekä hyödyntämään tätä tietoa laskemisessa, on hänen opittava useita erilaisia puhuttua ja kirjoitettua lukujärjestelmää koskevia sääntöjä ja periaatteita. Ymmärtääkseen paikka-arvoa ja kymmenjärjestelmää lapsen tulee osata luoda yhteyksiä lukusanojen, numerosymbolien, konkreettisten materiaalien ja kuvien muodostamassa verkostossa. Liittämällä paikka-arvo- ja kymmenjärjestelmäharjoituksiin elementtejä näistä kaikista neljästä osa-alueesta, voidaan tukea lapsen ymmärrystä lukujärjestelmästämme.
Paikka-arvon ja kymmenjärjestelmän periaatteita
Seuraavassa on kuvattu periaatteita, joita lapsen tulisi ymmärtää kymmen- ja paikkajärjestelmästä (esim. Lawton 2006, Haylock & Cockburn 2008).
Paikka-arvo
Järjestelmässämme on vain 10 numeromerkkiä (0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9), joilla voidaan muodostaa ääretön määrä erilaisia lukuja paikkajärjestelmää hyväksi käyttäen. Numeromerkin paikka luvussa ilmoittaa sen arvon. Oikeanpuoleisin paikka esittää ykkösiä, siitä seuraava vasemmalle kymmeniä, siitä seuraava satojen paikkaa ja niin edelleen, aina kymmenkertaisena edelliseen paikkaan verrattuna. Niinpä esimerkiksi numeron 8 arvo luvussa 800 on kymmenkertainen verrattuna lukuun 80.

Vaihtaminen
Kymmenen kappaletta yhtä lukuyksikköä voidaan vaihtaa yhteen vasemmanpuoleiseen lukuyksikköön tai päinvastoin yksi kappale yhtä lukuyksikköä voidaan vaihtaa kymmeneen oikeanpuoleiseen lukuyksikköön. Periaate havainnollistuu lapselle konkreettisen materiaalin ja kielentämisen kautta.

”Yksi näitä on kymmenen noita." "Yksi kymmensauva on kymmenen ykköspalaa.”
tai
”Kymmenen näitä on yksi noita." "Kymmenen ykköspalaa on yksi kymmensauva.”
Vaihtamisen periaatteen hyödyntäminen ja ymmärtämisen merkitys tulevat selkeästi esille myöhemmin opittavissa allekkainlaskuissa. Yhteenlaskuissa yhdestä lukuyksiköstä yli jääneet yksiköt ”annetaan” seuraavaan vasemmanpuoleiseen lukuyksikköön. (Esim. jos ykkösten 8 + 4 summa on 12, jätetään ykkösten paikalle ykköset eli 2 ja annetaan kymmenille yksi kymmen, joka merkitään muistinumerona kymmenien sarakkeen yläpuolelle.) Allekkain vähennettäessä puolestaan - jos paikalla ei ole tarpeeksi mistä vähentää - ”lainataan” eli vaihdetaan suurempi lukuyksikkö kymmeneen pienempään, jos kyseisellä paikalla ei ole tarpeeksi mistä vähentää (esim. jos ykkösten paikalla joutuisi vähentämään neljästä viisi, ”lainataan” kymmenistä yksi kymmenen, joka vaihdetaan kymmeneen ykköseen ja lisätään alkuperäisiin ykkösiin, jolloin voidaan suorittaa lasku 14 – 5). Tällöin on muistettava myös merkitä, että kymmeniä on tämän jälkeen yksi vähemmän.
Konkreettisen materiaalin yhdistäminen numerosymboleihin
Konkreettisen materiaalin ja numerosymbolien yhdistämistä voidaan havainnollistaa esimerkiksi käyttämällä valmiita kymmenjärjestelmävälineitä tai kuminauhalla niputettuja tikkuja sekä liittämällä niihin jokin 2- tai 3-numeroinen kirjoitettu luku (ks. harjoituksia alla).
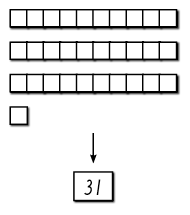
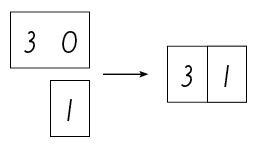
Lukujen muodostamista numerosymboleilla voidaan harjoitella päällekkäin laitettavilla numerokorteilla (ykköset, kymmenet ja sadat). Päällekkäin asetettavat numerokortit havainnollistavat lapselle mitä tapahtuu, kun kirjoitetaan luku, joka koostuu useammasta kuin yhdestä numerosymbolista. Tällöin havainnollistuu niin sanottu päälle kirjoittamisen sääntö.
Lukusanojen yhdistäminen numerosymboleihin
Lukujen kirjoittaminen ja sanominen eivät kulje aina käsi kädessä. Esimerkiksi kirjoitettuna luku 467 sanotaan ”neljäsataakuusikymmentäseitsemän”. Sanat ”sataa” ja ”kymmentä” eivät varsinaisesti näy kirjoitetussa luvussa, vaan lapsen tulee tietää, että numero 4 on satojen paikalla ja numero 6 kymmenien. Kun lapsi joutuu kirjoittamaan luvun joko konkreettisin materiaalein tai suullisesti esitetystä muodosta, yleisimpiä virheitä on luvun kirjoittaminen esimerkiksi seuraavilla tavoilla: 400607, 40067 tai 4067. Tällöin lapsi ei vielä osaa päälle kirjoittamisen sääntöä ja eikä tunne paikkojen merkitystä luvussa. Asiaa voidaan harjoitella konkreettisen materiaalin ja päällekkäin asetettavien numerokorttien kanssa ja liittää harjoitteluun lukujen kielentäminen (ks. harjoituksia alla).
Nolla
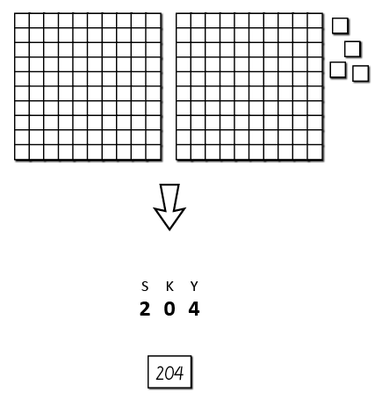
Nolla ilmaisee tyhjän lukuyksikön paikan. Konkreettisen materiaalin avulla voidaan havainnollistaa sitä, että luvussa ei aina ole kaikkia lukuyksiköitä ja silloin ”tyhjän kohdan” paikalle kirjoitetaan nolla. Lukusanoja sanottaessa nolla ei kuulu, mikä tekee lukusanojen kirjoittamisesta haasteellista osalle lapsista.
Harjoitustehtäviä paikka-arvon ja kymmenjärjestelmän ymmärtämiseen
Seuraavassa on esitetty harjoitustehtäviä, joita voidaan käyttää joko lapsiryhmän tai yksittäisen lapsen kanssa harjoiteltaessa paikka-arvoa ja kymmenjärjestelmää. Harjoitukset pohjautuvat Suomessa kehitettyyn kuntoutus- ja/tai opetusmenetelmään (Koponen & Mononen 2009) sekä seuraavaan kirjallisuuteen: Haylock & Cockburn 2008, Wright, Martland, Stafford & Stanger 2006 ja Cotter 2007.
Tehtävissä käytettäviä materiaaleja
| 10-järjestelmävälineet |
muoviset tai puiset välineet, jotka koostuvat ykköspaloista, kymmensauvoista, satalevyistä sekä tuhatkuutiosta |
| Tikut | kuminauhalla kymmenen tikun ryhmiin niputettuja tikkuja sekä irrallisia tikkuja (esim. askartelutikut) |
| Numerokortit (Lataa tulostettavat numerokortit tästä, pdf) |
numerot 1–9 sekä kymmen- ja sataluvut sekä tuhatkortti. Kortit voidaan asettaa päällekkäin oikeasta reunasta, jolloin muodostuu haluttu luku. |
| Satataulu (Lataa tulostettava satataulu tästä, pdf; lataa tulostettava tyhjä satataulupohja tästä, pdf) |
taulukko, jossa luvut 1–100 |
Harjoitustehtäviä
| Lukuyksiköt (tikut) | Tehtävään tarvitaan paljon tikkuja, joiden määrä tulee selvittää. Tikut niputetaan kymmenen tikun ryhmiin esim. kuminauhalla. Sata tikkua määritetään laskemalla tikut kymmenen ryhmissä (10, 20, 30… 100). Kymmenen kymmennippua sidotaan yhteen kuminauhalla. Lopuksi lasketaan tikkujen määrä - sadat, kymmenet, ykköset - ja merkataan lukumäärä numeroin. |
| Lukujen 1 – 100 muodostaminen numerokorteilla (numerokortit) |
Tehtävän avulla lapselle havainnollistetaan, kuinka kaksinumeroisissa luvuissa ykkösten paikalla olevat numerot vaihtuvat järjestyksessä 0:n ja 9:n välillä. Yhdeksän jälkeen vaihtuu aina seuraava tasakymmen, jossa ykkösten paikalla on 0. Lapsi asettaa pöydälle kymmenkortit allekkain ja viereen ykköskortit allekkain. Opettaja lähtee luettelemaan lukuja eteenpäin aloittaen ykkösestä. Kunkin sanotun luvun jälkeen lapsi muodostaa korteilla sanotun luvun. Aluksi voidaan luetella lukuja noin 30- 40:een asti, mutta haasteena voidaan kokeilla lukujen luettelua ja rakentamista sataan asti. |
| Luvun muodostaminen sanotun luvun mukaisesti (10-järjestelmävälineet, tikut tai numerokortit) |
Opettaja sanoo esim. ”34” ja lapsi rakentaa luvun välineillä (10-järjestelmävälineillä tai tikuilla) tai numerokorteista (30 ja 4 päällekkäin). |
| Luvun muodostaminen näytetyn luvun mukaisesti (10-järjestelmävälineet, tikut tai numerokortit) |
A) Opettaja näyttää numerokorteilla esim. luvun 89 ja lapsi rakentaa sen välineillä (10-järjestelmävälineillä tai tikuilla) ja sanoo luvun. B) Opettaja rakentaa luvun välineillä ja lapsi muodostaa sen numerokorteilla ja sanoo luvun. |
| Löydätkö luvun–peli (numerokortit) |
Numerokortit asetetaan epämääräiseen järjestykseen pöydälle (joko kaikki kortit, ykköset ja kymmenet tai kymmenet ja sadat). Opettaja sanoo lukuja, jotka lapsen tulee muodostaa korteista hieman sivummalle. ”Löydätkö luvun 30?” ”Löydätkö luvun 47?” Lapsi on osannut muodostaa luvut oikein, jos jäljelle jää viimeisenä kysytty luku. |
| Lisää 10 tai 100 välineillä (10-järjestelmävälineet tai tikut) |
A) Lapsi lisää aina kymmensauvan tai kymmenen tikun nipun, kun luettelee kymmenen lisää (10, 20, 30 jne.). Sadan kohdalla vaihdetaan kymmenen kymmensauvaa yhteen satalevyyn tai niputetaan kymmenen tikkunippua isoksi satanipuksi. B) Lapsi lisää aina satalevyn tai sadan tikun nipun, kun luettelee sata lisää (100, 200, 300 jne.). Tuhannen kohdalla vaihdetaan kymmenen satalevyä yhteen tuhatkuutioon tai niputetaan kymmenen sadan tikun nippua isoksi tuhatnipuksi. |
| Numerokortit (numerokortit) |
A) Lapsi järjestää numerokortit 10–100 järjestykseen ja näyttää ja sanoo järjestyksessä luvut etu- (ja taka)perin (10, 20, 30… 100). Tämän jälkeen yksi kortti voidaan kääntää lukujonosta ja lapsen on nimettävä käännetty kortti. B) Harjoitus tehdään samoin kuin tehtävä A, mutta korteilla 100–1000 (100, 200, 300…1000). |
| Aloituslukuna kymmeniä ja ykkösiä (10-järjestelmävälineet tai tikut) |
Aloitusluku on esim. 32. Lapsi rakentaa luvun ja sanoo sen. Lapsi lisää aina kymmensauvan tai kymmenen tikun nipun, kun luettelee kymmenen lisää (32, 42, 52 jne.) |
| Seuraava ja edellinen tasakymmen tai -sata (numerokortit) |
A) Kymmenkorteista on tehty pakka, joka on kuvapuoli alaspäin pöydällä. Lapsi kääntää kortin ja sanoo sovitusti seuraavan tai edellisen tasakymmenen (esim. lapsi kääntää luvun 50 ja sanoo 60). B) Harjoitus tehdään samoin kuin tehtävä A, mutta satakorteilla. Lapsi sanoo sovitusti edellisen tai seuraavan sataluvun. |
| Mikä luku on piilossa? (satataulu ja tyhjä satataulupohja) |
Opettaja peittää satataulusta joitakin lukuja esineellä tai paperin palalla (esim. 5, 25, 75, 85 ja 95) ja kysyy: ”Mikä luku on piilossa?” Sama voidaan tehdä myös tyhjällä satataululla. On tärkeää kysyä, miten lapset ratkaisevat ongelman (eli miten he laskevat satataulussa ja huomaavatko he säännönmukaisuuksia). Satataulua voidaan käyttää hyväksi myöhemmin yhteen- ja vähennyslaskuissa. Kun lisätään kymmeniä, liikutaan satataulussa ruutuja alaspäin. Kun vähennetään kymmeniä, ylöspäin. Ykkösiä lisätään liikkumalla oikealle ruudukossa ja vähennetään siirtymällä vasemmalle. Lukualueella 0–200 voidaan jatkaa satataulua kahteen sataan asti, laittamalla kaksi satataulua allekkain. |
| Missä on luku x? (tyhjä satataulu) |
Opettaja näyttää tyhjää satataulupohjaa ja kysyy: ”Missä kohdassa satataulua on luku 27?” Lapsi kirjoittaa luvun satataulupohjaan. On tärkeää kysymyksin selvittää, miten lapset ratkaisevat luvun paikan. ”Missä kohdassa on luku 37?” ”Entä 57?” ”Entä 17?” Jatketaan, kunnes kaikki luvut, joissa ykkösten paikalla on 7, on käsitelty. |
| Mikä on naapurin luku? (satataulu sekä paperi, jonka keskellä on yhden satataulun ruudun kokoinen aukko) |
Opettaja asettaa satataulun päälle paperin niin, että vain yksi luku (esim. 35) näkyy aukosta ja esittää kysymyksiä: ”Mikä on yläkerran naapurin luku?” (25) ”Mikä on alakerran naapurin luku?” (45) ”Mikä on oikealla olevan naapurin luku?” (36) ”Mikä on vasemmalla olevan naapurin luku?” (34) |
| Yksi lisää, yksi pois (10-järjestelmävälineet tai tikut, satatauluja) |
A) Yksi lisää. Opettaja rakentaa luvun, joka päättyy numeroon 9 tai numeroihin 99, esim. 39, 249 tai 599. Lapsi nimeää ja kirjoittaa luvun. Opettaja pyytää lasta lisäämään yhden ykköspalan tai tikun joukkoon ja sanomaan ja kirjoittamaan uuden luvun. Tehtävässä syntyy aina uusi kymmen tai sata, jolloin lapsen tulee vaihtaa kymmenen yksikköä suurempaan yksikköön (esim. 10 ykköstä yhteen kymmensauvaan). Tehtävä tarkistetaan etsimällä satataulusta aloitusluku ja liikkumalla yksi eteenpäin. Kolminumeroisissa luvuissa voidaan käyttää useampaa satataulua: ”täysi” sata voidaan kääntää kuvapuoli alaspäin pöydälle. B) Yksi pois. Tehtävä tehdään kuten tehtävä A, mutta nyt aloitusluku on jokin tasakymmen tai tasasata, esim. 50, 240 tai 600 ja luvusta vähennetään yksi pois. |



