Lukumääräisyyden taju
Synnynnäinen taito
Lukumääräisyyden taju on synnynnäinen taito, mikä löytyy sekä vastasyntyneiltä lapsilta, että eläimiltä. Koirien ja kissojen omistajilla on kokemuksia siitä, että heidän lemmikkinsä ymmärtää lukumäärien välisiä eroja. Näin todellakin on. Lähes poikkeuksetta on tutkimuksissa todettu, että eri eläinlajeilla on kyky hahmottaa lukumääriä. Lukumäärien hahmottamista ei ole tarvinnut eläimille opettaa, vaan niillä näyttäisi olevan myötäsyntyinen kyky määrien hahmottamiseen.
Varsinaisesta laskemisesta ei tässä kyvyssä ole kuitenkaan kyse. Kyse on suhteellisesta, epätarkasta, lukumäärien hahmotuskyvystä (Deahene, Spelke, Pine, Stanescu & Tsvikin, 1999; Lemer, Spelke & Cohen, 2003). Se on aistikanavasta riippumaton kyky erottaa toisistaan erilaisia ärsykkeitä jonkin piirteen mukaan.
Kuva. Alla olevista kuvapareista ensimmäisessä on vaikea erottaa, kummassa on enemmän palloja. Jälkimmäisestä kuvasta se on kuitenkin helppoa siitäkin huolimatta, että siniset pallot muodostavat pinta-alaltaan suuremman kokonaisuuden. Määrän ja pinta-alan vertailu ovat siis toisistaan erillisiä prosesseja.
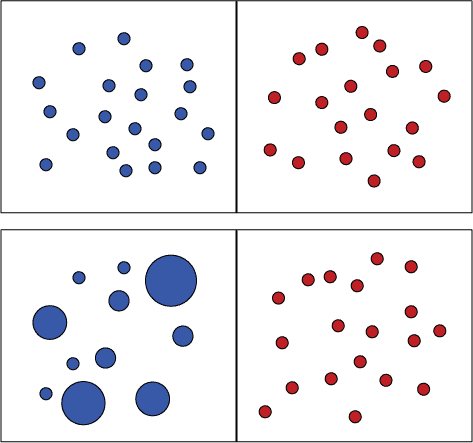
Pienten lasten erottelukyky kehittyy asteittain
Mitä suurempi ero lukumäärien välillä on, sitä helpompaa on ne erottaa toisistaan. Tutkimuksissa on havaittu, että alle 9-kuukautiset vauvat pystyvät hyvin erottamaan toisistaan 8 vs 16, vaikka pinta-ala olisikin kontrolloitu. Yli 11-kuukautiset vauvat pystyvät jo erottelemaan toisistaan jo 8 vs 12. Tämä erottelukyky näyttäisi paranevan kohtuullisesti aina varhaislapsuuteen saakka, jonka jälkeen kehitys tasaantuu.
Missään vaiheessa tämä hahmotuskyky ei muutu täysin tarkaksi. Ainoa keino tarkkaan määrän hahmottamiseen on kieli ja laskeminen. Sen voi helposti todeta esimerkiksi siten, että kysyy itseltään kuinka paljon kuvissa on punaisia ja sinisiä palloja. Ne on pakko laskea luettelemalla, eli käyttämällä kieltä ja laskemista (Gordon, 2004; Pica, Lemer, Izard & Deahene 2004).
Lukumääräisyyden hahmotuskyky ja matemaattiset taidot
Yksilöiden välillä on eroja siinä, miten "tarkka" heidän ei-kielellinen likimääräinen hahmotuskykynsä on. Viimeisimmät tutkimushavainnot viittaavat siihen, että tämä likimääräisen hahmotuskysyn tarkkuus tai epätarkkuus voisi selittää vaikeimpien matemaattisten oppimisvaikeuksien (dyskalkulia) kehityksen. Teorian lähtökohtana on, että likimääräisen hahmotuskyvyn tuoma kokemus lukumäärästä on perusta ymmärtää symbolein esitettyjen lukujen merkitys. Mikäli tämä likimääräinen hahmotuskyky on hyvin epätarkka, niin lukujen välisten suuruussuhteiden hahmottaminen ei kehity hyvin.



