Yksinumeroisilla luvuilla laskeminen
Aritmeettisten taitojen yleinen kehitys
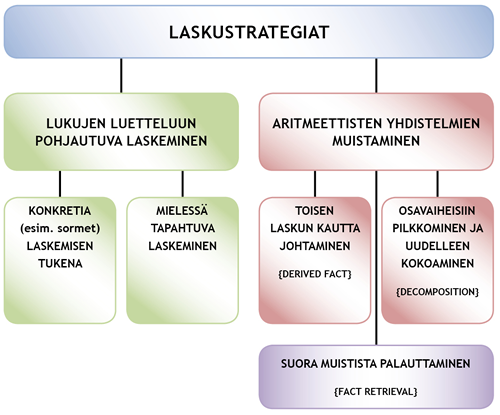
Aritmeettisten taitojen, yhteen-, vähennys-, kerto- ja jakolaskutaidon, kehittymistä voidaan kuvata eri laskustrategioiden käytön kautta (esim. Baroody, 1984; Fennema, Carpenter, Jacobs, Franke & Levi, 1998; Fuson, 1984; Geary, Bow-Thomas, Liu & Siegler, 1996), sillä laskustrategioiden käytössä voidaan nähdä tietty kehityksellinen järjestys. Osana laskutaidon kehittymistä lapsi keksii uusia laskustrategioita ja voi samalla jättää jonkin varhemmin oppimansa strategian pois käytöstä. Laskutaidon kehittymistä voidaankin kuvata erilaisten strategioiden suhteellisen osuuden avulla, esimerkiksi seuraamalla, missä määrin lapsi hakee vastauksia muististaan ja missä määrin ratkaisee ne luettelemalla laskien.
Eri laskutoimitusten välillä on eroa sen suhteen, miten paljon niiden opettelussa painottuu muistista haku tai erilaiset laskemisen strategiat. Esimerkiksi kertotaulun opettelu pohjaa vahvimmin ulkoaoppimiseen ja siinä muistista hakeminen on keskeisin strategia. Vastaavasti vähennyslaskussa ja jakolaskussa ulkoaoppiminen ei ole yhtä merkittävä apukeino ja niitä ratkotaan suhteessa enemmän erilaisten laskustrategioiden avulla käyttäen apuna yhteenlaskua ja kertolaskua.
Myös eri laskutoimitusten sisällä lapsi yleensä käyttää erilaisia strategioita; strategian valintaan vaikuttavat esimerkiksi laskun tekijät. Jo esikouluiässä lapsi saattaa muistaa ulkoa vastaukset osaan ”pienistä” laskuista, joiden summa on alle kymmenen. Vastaavasti osa laskuista, joissa vaaditaan kymmenen ylitystä (8 + 7, 6 + 9), ovat hankalampia, ja vanhempikin lapsi saattaa joutua ratkaisemaan ne laskemalla ulkoa muistamisen sijaan. Eri aritmeettisissa operaatioissa luvun 0 ja 1 sisältävien laskujen (esim. 4 + 0 tai 6 x 0) ajatellaan olevan poikkeuksellisia siinä mielessä, että niiden opettelu näyttäisi muita laskuja vahvemmin nojaavan sääntöihin, kuten ”jos lukuun lisätään tai siitä vähennetään nolla, on vastauksena luku itse”.
Lapsen käyttämät strategiat saadaan selville seuraamalla lapsen laskemista ja pyytämällä häntä selittämään, miten hän on ratkaissut jonkin laskutehtävän. Tavallisesti lapsilla on käytössään useita erilaisia strategioita. Sujuvaa laskijaa kuvaa se, että hän pääasiassa palauttaa nopeasti vastauksen muistista, mutta kykenee myös tarvittaessa valitsemaan muista strategioista sopivimman. Niillä lapsilla, joilla on matematiikan oppimisen vaikeuksia, on pääasiallisessa käytössä vain hitaita luetteluun pohjautuvia strategioita. Aritmeettisten yhdistelmien muistamiseen perustuvat ratkaisumallit ovatkin näille lapsille usein vaikeita. Tutkimukset osoittavat, että vaikeus oppia ja muistaa aritmeettisia yhdistelmiä on luonteeltaan varsin pysyvä eivätkä vaikeudet laskemissa häviä iän myötä itsestään vaan tukitoimia tarvitaan. Lapsi tarvitseekin aikuisen ohjausta oppiakseen nopeampia ja tehokkaampia laskemisen strategioita (ks. osiosta tukitoimet).
Yhteen- ja vähennyslaskutaidon kehittyminen
Yhteen- ja vähennyslaskutaidot kehittyvät asteittain. Laskutaito kehittyy luetteluun pohjautuvan laskemisen kautta kohti aritmeettisten yhdistelmien muistamista. Lapsi käyttää ja kokeilee laskustrategioita spontaanisti ja oppii niitä myös kouluopetuksessa (Steinberg, 1985; Thornton, 1978; Thornton 1990). Vähennyslaskustrategiat ovat lapselle vaikeampia kuin yhteenlaskustrategiat – sekä spontaanisti että kouluopetuksessa opittaviksi (Steinberg, 1985). Vähennyslaskuissa pitää muistissa pitää useampia vaiheita kuin yhteenlaskussa. Vähennyslaskustrategioiden käytössä auttaa yhteen- ja vähennyslaskun välisen suhteen ymmärtäminen.
Lukujen luetteluun pohjautuva laskeminen yhteen- ja vähennyslaskussa
Aluksi lapsi ratkoo laskutehtäviä lukujen luetteluun pohjautuvien strategioiden kautta. Lapsi laskee aluksi konkretian ja visuaalisen tuen avulla (kuten esineet, sormet ja piirtäminen) ja siirtyy sitten käyttämään pelkästään mielessä tapahtuvaa laskemista lukujonoja luettelemalla (Ostad, 1999; Siegler & Shrager, 1984; Siegler, 1987). Strategian käytössä voidaan erotella myös se, miten lapsi laskee luettelemalla eli kuinka paljon lukuja lapsi luettelee ja mistä luvusta hän lähtee laskemisessaan liikkeelle.
Alkuvaiheessa lapsi laskee laskun kaikki tekijät yksitellen esineillä tai sormilla ja samoin myös vastauksen (esim. 2 + 4 à 1, 2 ― 1, 2, 3, 4 ― 1, 2, 3, 4, 5, 6). Myöhemmin lapsi aloittaa laskemisen keskeltä lukujonoa (2 + 4 à 2 ― 3, 4, 5, 6). Tässä vaiheessa lapsen lukujonotaidot ovat kehittyneet niin, että luettelun aloittaminen keskeltä lukujonoa on mahdollista. Tehokkaammasta tavasta laskea kertoo se, että lapsi luettelee mahdollisimman vähän lukuja, esimerkiksi aloittaa laskemisen suuremmasta luvusta (esim. 2 + 4 à 4 ― 5, 6). Lapsen kanssa on hyvä käydä läpi yhteenlaskun vaihdannaisuuslakia (yhteenlaskettavien järjestys ei muuta laskun vastausta, 2 + 4 = 4 + 2). Tällöin lapsi voi oppia hyödyntämään sitä laskemisessaan. Vähennyslaskussa saman hyödyntäminen edellyttää yhteenlaskun yhteyden ymmärtämistä. Esimerkiksi laskussa 9 - 7 on nopeampaa ja tehokkaampaa laskea seitsemästä eteenpäin yhdeksään (8, 9 à vastaus on 2) kuin laskea taaksepäin yhdeksästä seitsemän pois (8, 7, 6, 5, 4, 3, 2). Kun lapsi ei käytä enää laskemisen tukena esineitä, joutuu hän pitämään muistissaan sekä tietoa siitä, kuinka monta hän on jo lisännyt tai vähentänyt, sekä siitä, mikä missäkin laskuvaiheessa on vastaus (esim. 5 + 3 à 1 lisää on 6, 2 lisää on 7, 3 lisää on 8).
Laskujen ratkaiseminen mielessä luetteluun pohjautuvien strategioiden avulla on siis monivaiheinen suoritus. Laskujen ratkaiseminen edellyttää lapselta monia yhtäaikaisia toimintoja ja asioiden pitämistä muistissa. Siksi on tärkeää, että lapsi osaa luetella sujuvasti eteen- ja taaksepäin lukujonoa ja aloittaa luettelemisen annetusta luvusta (Baroody, 1984).
Lukujen luetteluun pohjautuva laskeminen on työlästä, hidasta ja virhealtista. Lapsi käyttää kuitenkin esimerkiksi sormiaan laskemisen tukena, kunnes on kehittynyt taidoissaan niin, että pystyy laskemaan vain mielessään ja myöhemmin hakemaan nopeasti aritmeettisia yhdistelmiä muististaan.
Lukujen luetteluun pohjautuvat strategiat yhteenlaskussa
Konkretia tai visuaalinen tuki laskemisen apuna
(mukailtu Ostad, 1999)
| Laske kaikki, aloita alusta | Esim. 3 + 2 = ? Lapsi laskee kolme esinettä yksitellen "1,2,3". Hän lisää yksitellen laskien kaksi esinettä "1,2", laskee sitten alusta kaikki esineet "1,2,3,4,5" ja saa tulokseksi viisi. |
| Laske toinen luvuista, aloita alusta |
Esim. 3 + 4 = ? Lapsi näyttää sormillaan suoraan luvun 3 ja lisää siihen luetellen neljä lisää "1, 2, 3, 4". Sitten hän laskee alusta kaikki sormet tai katsoo vastauksen suoraan sormien lukumäärästä. |
| LAske eteenpäin |
Esim. 4 + 3 = ? Lapsi näyttää sormillaan luvun 4 ja laskee eteenpäin sormien avulla "5, 6, 7". Vastauksena on viimeiseksi sanottu lukusana. |
| LAske eteenpäin, aloittaen suuremmasta luvusta |
Esim. 2 + 5 = ? Lapsi aloittaa laskemisen suuremmasta luvusta. Hän näyttää sormillaan luvun viisi ja laskee sormien avulla eteenpäin "6, 7". Vastaus on viimeiseksi sanottu lukusana. |
Mielessä tapahtuva laskeminen
(Carpenter & Moser, 1984)
| Laske eteenpäin ensimmäisestä luvusta |
Esim. 3 + 4 = ? Lapsi aloittaa luvusta 3 ja laskee mielessään eteenpäin "4, 5, 6, 7". Vastaus on viimeiseksi sanottu lukusana. |
| laske eteenpäin suuremmasta luvusta |
Esim. 2 + 5 = ? Lapsi aloittaa laskemisen suuremmasta luvusta. Hän sanoo luvun viisi ja laskee mielessään eteenpäin "6, 7". Vastaus on viimeiseksi sanottu lukusana. |
Lukujen luetteluun pohjautuvat strategiat vähennyslaskussa
Konkretia tai visuaalinen tuki laskemisen apuna
(mukaeltu Ostad, 1999)
| laske kaikki, aloita alusta | Esim. 5 – 3 = ? Lapsi laskee viisi esinettä yksitellen. Sitten hän laskee pois kolme esinettä, laskee jäljelle jääneet ja saa tulokseksi kaksi. |
| Laske eteenpäin | Esim. 7 – 4 = ? Lapsi aloittaa luvusta 4, laskee eteenpäin sormien tuella ”5, 6, 7”. Vastaus on lueteltujen lukujen määrä eli kolme. |
| Laske taaksepäin annetun luvun verran | Esim. 8 – 3 = ? Lapsi aloittaa laskemisen luvusta 8 ja laskee sormien avulla taaksepäin kolme lukua ”7, 6, 5”. Vastaus on viimeiseksi sanottu luku. |
| Laske eteen- tai taaksepäin | Lapsi valitsee laskun ratkaisemisen tavaksi edellä esitellyistä kohdista joko kohdan 2 tai 3 riippuen siitä, kummalla tavalla tarvitsee laskea vähemmän. Esim. laskussa 9 – 7 = ? lapsi valitsisi kohdan 2. |
Mielessä tapahtuva laskeminen
(mukaeltu Fuson, 1984 ja Ostad, 1999)
| Laske eteenpäin |
Esim. 7 – 4 = ? Lapsi aloittaa luvusta 4, laskee eteenpäin mielessään ”5, 6, 7”. Vastaus on lueteltujen lukujen määrä eli kolme. |
| Laske taaksepäin annetun luvun verran | Esim. 8 – 3 = ? Lapsi aloittaa laskemisen luvusta 8 ja laskee mielessään taaksepäin kolme lukua ”7, 6, 5”. Vastaus on viimeiseksi sanottu luku. |
| LAske taaksepäin annettuun lukuun asti |
Esim. 8 - 6 =? Lapsi aloittaa laskemisen luvusta 8 ja laskee mielessään taaksepäin lukuun 6 asti "7, 6". Vastaus on lueteltujen lukujen määrä eli 2. |
| LAske eteen- tai taaksepäin |
Lapsi valitsee laskun ratkaisemiseen edellä esitellyistä kohdista joko kohdan 2, 3 tai 4, riippuen siitä millä tavalla tarvitsee laskea vähiten. Esim. laskussa 9 - 7 = ?, lapsi valitsisi kohdan 2 tai 4. |
Aritmeettisten yhdistelmien muistaminen yhteen- ja vähennyslaskussa
Kun lapsi käyttää laskustrategioita onnistuneesti yhteen- ja vähennyslaskuissa, laskun tekijöiden ja vastauksen välille muodostunut yhteys vahvistuu vähitellen (Barrouillet & Fayol, 1998; Siegler & Shrager, 1984). Tällöin lapsi voi palauttaa muististaan suoraan laskun vastauksen (esim. 2 + 3 = 5). Toisaalta lapsi voi käyttää osaamiaan aritmeettisia yhdistelmiä hyväkseen ratkaistessaan laskutehtäviä. Lapsi voi johtaa laskun vastauksen jonkin tuntemansa yhdistelmän kautta (esim. 6 - 3 = 3, joten 6 - 4 = 2, koska luku neljä on yhden suurempi kuin luku kolme). Lapsi voi myös pilkkoa laskun osavaiheisiin ja koota laskun uudelleen niin, että käyttää hyväkseen tuntemiaan yhdistelmiä ja tietojaan lukujärjestelmästä, kuten 7 + 5 à 7 + (3 + 2) à 10 + 2 = 12.
Eräiden tutkijoiden mukaan (mm. Putnam ym., 1990; Thornton, 1990; Carpenter & Moser, 1984) laskun johtaminen toisen laskun kautta voi edesauttaa aritmeettisten yhdistelmien oppimista ja suoraan muistista palauttamista. Esimerkiksi lapselle opetetaan ensin muihin laskuihin nähden melko helposti opittavat ns. tuplat (yhteenlaskettavana on kaksi kertaa sama luku, esim. 4 + 4) ja niitä hyödyntämällä opetetaan muita lähellä olevia aritmeettisia yhdistelmiä (kuten 4 + 4 = 8, joten 4 + 5 = 9). Toisen laskun kautta johtamista sekä lukujen osavaiheisiin pilkkomista voidaan havainnollistaa aluksi lapselle konkreettisilla tai visuaalisilla materiaaleilla.
Yleensä lapset oppivat käyttämään muistista palautettavia yhdistelmiä pääasiallisena laskustrategianaan noin yhdeksään ikävuoteen mennessä (Ashcraft & Fierman, 1982; Brauwer, Verguts, & Fias, 2006; Lemair & Siegler, 1995). Laskustrategioiden kehittyneimmällä tasolla lapsi palauttaa laskun vastauksen muististaan nopeasti (noin 2–3 sekunnissa). Näitä suoraan muistista palautettavia yhdistelmiä lapsi voi käyttää apuna laskemisessaan sellaisissa laskuissa, joihin hän ei vielä muista vastausta. Kun suuria lukuja lasketaan allekkain, pienten laskujen ulkoamuistaminen on entistä tärkeämpää. Jos laskeminen ei käy sujuvasti lukualueella 0–20, on allekkainlaskujenkin tekeminen hidasta. Ylipäätään lukualueella 0–20 sujuva, automatisoitunut laskeminen on edellytys suurten lukujen laskemiseen.
Toisen laskun kautta johtaminen yhteenlaskussa
(mukailtu Steinberg, 1985)
| Tupla +1, +2 |
Käytetään hyväksi tunnettua tuplaa ja lisätään siihen yksi tai kaksi esim. 6 + 7 = (6 + 6) + 1 = 13 |
| tupla -1, -2 |
Käytetään hyväksi tunnettua tuplaa ja vähennetään siitä yksi tai kaksi esim. 7 + 6 = (7 + 7) - 1 = 13 |
| kymppiparit | Käytetään hyväksi opittuja kymppipareja. esim. 8 + 2 = 10, joten 8 + 3 = 11 |
| 10-lasku | Käytetään apuna 10-laskua, jossa toisena tekijänä on 10. esim. 10 + 8 = 18, joten 9 + 8 = 17 |
| Jaettu | Yhteenlasku havainnollistuu hyvin palikoilla, kun toisesta palikkapötköstä siirretään yksi palikka toiseen, jolloin saadaan tupla. Myöhemmin tästä syntynyttä mielikuvaa voidaan käyttää hyväksi laskemisessa. esim. 7 + 5 = 6 + 6 |
| Toisen tunnetun yhdistelmän kautta |
Esim. 7+5=(7+4)+1=12 |
Toisen laskun kautta johtaminen vähennyslaskussa
Yhteenlaskun kautta tapahtuvia johtamisia vähennyslaskussa
(mukailtu Steinberg, 1985)
| Tupla +1 |
Käytetään hyväksi tunnettua tuplaa ja lisätään siihen yksi. esim. 13 - 6 --> 6 + __ = 13 --> 6 + (6 + 1) = 13 |
| tupla -1 |
Käytetään hyväksi tunnettua tuplaa ja vähennetään siitä yksi. esim. 11 - 6 --> 6 + __ = 11 --> 6 + (6 - 1) = 11 |
| Jaettu | Yhteenlasku havainnollistuu hyvin palikoilla, kun toisesta palikkapötköstä siirretään yksi palikka toiseen, jolloin saadaan tupla. Tätä mielikuvaa käytetään hyväksi myös vähennyslaskussa. esim. 12-7 --> 6+6=12, joten 7+5=12 |
Vähentämisen kautta tapahtuvia johtamisia vähennyslaskussa:
| 10-lasku |
Käytetään apuna 10-laskua, jossa toisena tekijänä on 10. esim. 16 - 10 = 6, joten 16 - 9 = 7 |
| Toisen tunnetun yhdistelmän kautta | esim. 12 - 7 --> 12 - 8 = 4, joten 12 - 7 = 5 |
Osavaiheisiin pilkkominen ja uudelleen kokoaminen yhteenlaskussa
| Lisääminen 10 kautta |
Luku täydennetään ensin kymmeneen ja katsotaan kuinka paljon tulee vielä kymmenen yli lisää. esim. 8 + 5 --> (8 + 2) + 3 = 10 + 3 = 13 |
Osavaiheisiin pilkkominen ja uudelleen kokoaminen vähennyslaskussa
(Steinberg, 1985)
| Lisääminen 10 kautta |
Luku täydennetään ensin kymmeneen ja katsotaan kuinka paljon tulee vielä kymmenen yli lisää. 13 - 6 --> 6 + 4 = 10, 10 + 3 = 13 --> 4 + 3 = 7 |
| Vähentäminen 10 kautta |
Luku vähennetään ensin kymmeneen ja otetaan vielä jäljelle jäänyt kymmenestä pois. 12 - 7 --> 12 - 2 = 10, 10 - 5 = 5 |
| Vähentäminen kymmenestä |
Otetaan kymmenen yli menevä luku "talteen", sen jälkeen otetaan vähentäjä pois kymmenestä ja lisätään talteen laitettu luku muistista. 12 - 4 = (10 - 4) + 2 = 8 |
Keinoja yhteenlaskustrategioiden opettamiseen
Keinoja vähennnyslaskustrategioiden opettamiseen
Kerto- ja jakolaskutaidon kehittyminen
Kertolasku poikkeaa yhteen- ja vähennyslaskusta siinä mielessä, että oppimisprosessi on suoraviivaisempi ja harjoittelussa korostuukin suuremmassa määrin ulkoa opettelu. Kertolaskutaidon tyypillisessä kehityksessä keskeinen ratkaisutapa heti taidon opettelun alkuvaiheesta lähtien on vastauksen hakeminen suoraan muistista.
Aritmeettisista operaatioista selkeästi vähiten tutkittu on jakolasku. Alussa lapset näyttäisivät tukeutuvan toistuvaan yhteenlaskuun, mutta kertolasku nousee nopeasti yleisimmäksi tavaksi ratkaista jakolasku. Jakolaskutaidon kehittymisen kannalta keskeistä onkin kertolaskun hyvä hallinta sekä kerto- ja jakolaskun välisen yhteyden ymmärtäminen. Käytännössä jakolaskujen laskeminen on hyvin hankalaa ja työlästä, ellei lapsi hallitse kertolaskuja. Tämä on tärkeä pitää mielessä, kun mietitään, mistä laskutaidon tukemisessa lähdetään liikkeelle.
Lukujen luetteluun pohjautuva laskeminen kerto- ja jakolaskussa
Kertolaskun opettelun alkuvaiheessa lapset käyttävät melko yleisesti strategianaan toistuvaa yhteenlaskua ja lukujonon luettelemista tietyn askeleen välein. Osa lapsista pystyy ääneen tai mielessään liikkumaan lukujonossa ilman visuaalista tukea esimerkiksi viiden askelen välein (esim. 4 x 5 à 5, 10, 15, 20). Lapset voivat käyttää myös sormiaan tukena luettelussa, esimerkiksi auttamaan pysymään selvillä, montako harppausta lukujonossa on menty (”viisi” à yksi sormi, ”kymmenen” à toinen sormi jne.). Osa lapsista ei pysty kuitenkaan liikkumaan lukujonossa harppauksittain vaan joutuu ratkomaan kertolaskuja laskemalla yksitellen. Lapsi esimerkiksi piirtää ryhmiä viivoista ja laskee niitä. Kertolaskun ratkaisemisessa yksittäisten esineiden tai viivojen laskeminen ei ole mielekästä, vaan tällöin ensisijaisena lähtökohtana on tukea lapsen lukujono- ja yhteenlaskutaitoa sekä selkeyttää kertolaskun käsitettä.
Jakolaskussa luettelupohjaisiin strategioihin voidaan puolestaan laskea toistuva yhteenlasku, jossa jakajaa lasketaan yhteen, kunnes saavutetaan jaettava, tai vähennyslasku, jossa puolestaan jaettavasta vähennetään jakajan osoittamaa määrää, kunnes päädytään nollaan. Näitä kahta muistuttava strategia on ryhmittely, jossa lapsi ratkaisee, kuinka monta jakajan suuruista ryhmää jaettavasta saadaan.
Aritmeettisten yhdistelmien muistaminen kerto- ja jakolaskussa
Kertolaskussa yleisimmäksi strategiaksi nousee melko nopeasti aritmeettisten yhdistelmien hakeminen suoraan muistista. Kansainvälisissä tutkimuksissa on osoitettu, että jo toisella luokalla muistista hakeminen on yleisin ratkaisutapa ja lapset käyttävät sitä yli puolessa kertolaskuista. Neljännellä luokalla (noin 9 vuoden iässä) lapset ratkaisevat kertolaskut suurimmaksi osaksi (noin 70–80-prosenttisesti) hakemalla vastauksen muistista.
Toisena muistista hakuun pohjautuvana strategiana kertolaskussa on toisen laskun avulla johtaminen.
Jakolaskussa käytettyjä muistiin pohjautuvia strategioita ovat vastauksen hakeminen suoraan muistista, laskeminen kertolaskun avulla sekä laskun jakaminen pienempiin helpommin ratkaistaviin laskuihin. Jakolasku näyttäisi olevan aritmeettisista operaatioista ”vähiten automatisoituva”. Esimerkiksi Kanadassa tehdyssä tutkimuksessa vähän vanhemmatkin oppilaat (kuudes–seitsemäsluokkalaiset) käyttivät vastauksen hakemista muistista jakolaskustrategianaan selvästi harvemmin kuin kertolaskua.



