Matemaattiset oppimisvaikeudet ja työmuisti

Matematiikan oppimiseen ja matemaattisissa tehtävissä suoriutumiseen tarvitaan varsinaisten matemaattisten taitojen lisäksi erilaisia yleisiä tiedonkäsittelyresursseja kuten työmuistia. Työmuisti yksinään ei ratkaise matemaattisia ongelmia, mutta osana tiedonkäsittelyjärjestelmää se on välttämätön. Se toimii laskemisessa aktiivisena prosessointi- ja varastointitilana, ja toisaalta se tarjoaa resursseja matemaattisten tietojen ja taitojen kehittymiseen (ks. myös Service & Lehto, 2002).

Tämän matemaattiset oppimisvaikeudet ja työmuisti -tekstin on kirjoittanut palveluumme kutsuttuna kirjoittajana FT Minna Kyttälä Helsingin yliopistosta.

Työmuisti voidaan ajatella työtilaksi, jossa tehtäviä, tehtävänosia ja laskuvaiheita varastoidaan ja työstetään (ks. esim. Heathcote, 1994). Työmuistin kapasiteetin puutteet tarkoittavat puolestaan sitä, että näitä toimintoja varten on vähemmän tilaa. Työtilan puute saattaa vaikeuttaa tehtävän ratkaisemista, tiedon siirtymistä säilömuistiin (pitkäkestoiseen muistiin) ja matemaattisen tiedon hakua säilömuistista (ks. Service & Lehto, 2002). Tämä kaikki hankaloittaa matemaattisissa tehtävissä suoriutumista ja matematiikan oppimista.

Mikä on työmuisti?

Työmuisti vastaanottaa, käsittelee ja varastoi informaatiota lyhytaikaisesti (Baddeley, 1986, 1997). Se tulkitsee, yhdistää ja muokkaa vastaanottamaansa ja hetkellisesti varastoimaansa informaatiota eli se käsittelee tietoa aktiivisesti. Se pitää siis sisällään kaiken sen tiedon, jota tarvitsemme meneillään olevien kognitiivisten tehtävien suorittamiseen. Työmuisti ei ole konkreettinen elin eikä selvärajainen erillinen aivoalue vaan pikemminkin tiettyjen aivoalueiden yhteistä työskentelyä. Työmuistilla tarkoitetaan lyhytkestoista aktiivista tiedonkäsittelyä ja käsiteltävän tiedon varastointia.

Työmuisti on kapasiteetiltaan rajallinen, eikä se pysty kerralla käsittelemään kaikkea saatavilla olevaa informaatiota eikä välttämättä kaikkea kulloisenkin tehtävän kannalta oleellistakaan informaatiota. Työmuistin kapasiteetiksi on tuoreimmissa tutkimuksissa arvioitu 3–5 yksikköä, mutta yksikön sisältämä informaatiomäärä ei ole vakio: yksi yksikkö voi sisältää vaihtelevan määrän informaatiota.

Esimerkki: Lukusarja 6 4 3 7 5 2 sisältää kuusi yksikköä informaatiota. Jos vierekkäiset luvut yhdistetään, yksiköiden määrä onkin enää kolme: 64 37 52.

Ihmisten työmuistikapasiteetit ovat erilaisia. Yksilöiden väliset erot eivät ole yksinomaan absoluuttisessa kapasiteetissa (eli siinä, että toinen muistaa 2 ja toinen 6 yksikköä) vaan myös siinä, että toiset yksilöt pystyvät tehokkaammin pakkaamaan informaatiota tiiviiseen tilaan yhdistämällä pieniä asioita suuremmiksi kokonaisuuksiksi. Tässä pienten yksiköiden yhdistämisessä auttaa esimerkiksi kokemus: asiantuntijan on todennäköisesti muita ihmisiä helpompi hahmottaa alaansa kuuluvia asioita isoina kokonaisuuksina (ks. esim. Kalakoski, 2006). Sama pätee myös matematiikkaan: aiempi oppimisvaranto tarjoaa pohjaa isompien viipaleiden muodostamiselle. Kokenut osaaja pystyy niputtamaan informaatiota monin eri tavoin ja siten säätelemään työmuistia kuormittavan informaation määrää.

Esimerkki: 5·5 <=> 5+5+5+5+5 <=> 5² <=> 10+10+5 <=> 25
Esimerkki: Tehtävänanto: Laske ruokaostosten loppusumma, kun ostoksia tehdään seuraavasti: viisi banaaninippua (á 5 €), kolme leipää (á 5 €) ja viisi maitoa (á 1 €). Tehtävän voi ratkaista monin eri tavoin, esimerkiksi 5∙5 + 3∙5 + 5∙1 tai 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 1 + 1 + 1 + 1 + 1 tai 25 + 15 + 5. Nämä eri laskutavat kuormittavat työmuistiresursseja hyvin eri tavoin. Mitä kokeneempi laskija on, sitä tehokkaammin hän pystyy niputtamaan yksityiskohtaista tietoa suuremmiksi kokonaisuuksiksi, jolloin työmuistiresurssit kuormittuvat vähemmän.

Yksi tutkituimpia työmuistimalleja on Baddeleyn (1986, 1997) kolmikomponenttimalli, jossa lyhytkestoisen tiedon käsittely ja varastointi jaetaan informaation luonteen mukaan. Mallissa on kolme komponenttia, joista työmuistin keskusyksikkö on työmuistin aivot. Se huolehtii korkeamman tason prosessointitoiminnoista, kuten toimintastrategioiden valinnasta ja tarkkaavaisuuden suuntaamisesta sekä kahden muun varastojärjestelmän toiminnan valvomisesta ja säätelemisestä. Kaksi apujärjestelmää ovat fonologinen silmukka, joka vastaa kielellisen, auditiivis-fonologisen informaation varastoinnista, ja visuaalis-spatiaalinen luonnoslehtiö, joka nimensä mukaisesti varastoi lyhytaikaisesti visuaalista ja avaruudellista informaatiota. Myöhemmin Baddeley (2000) on täydentänyt mallia yhdellä uudella komponentilla, episodisella puskurilla (episodic buffer), jonka oletetaan mm. yhdistävän informaatiota alajärjestelmien ja säilömuistin välillä.

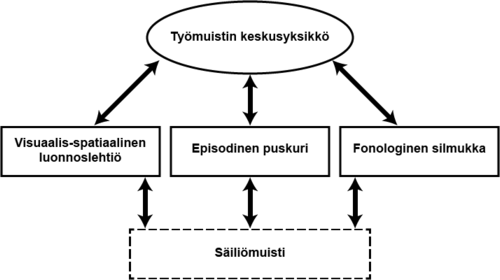
: Kuva 1. Baddeleyn (1986, 1997, 2000) kolmikomponenttimalli täydennettynä episodisella puskurilla.

Yksinkertaistettuna työmuisti voidaan siis jakaa kielelliseen ja visuaalis-spatiaaliseen järjestelmään, joita kontrolloi ja ohjaa yksi keskusyksikkö. Nämä alueet voivat olla eri tavoin kehittyneitä: jonkun fonologiset työmuistiresurssit voivat olla heikot ja silti samanaikaisesti visuaalis-spatiaaliset resurssit vahvat tai toisinpäin.

Työmuistin kehittyminen

Kunkin työmuistikomponentin kapasiteetti kasvaa voimakkaasti iän myötä aina nuoruusvuosiin eli noin 15–16 vuoden ikään asti (ks. esim. Lehto ym., 2003; Logie & Pearson 1997; Siegel, 1994; Wilson ym., 1987). Visuaalis-spatiaalisen työmuistin kapasiteetin (lähinnä passiivisen varastoinnin) kehittyminen vaikuttaa olevan suhteellisen riippumaton fonologisen työmuistin kapasiteetin kehittymisestä, joskin kehittyminen on samansuuntaista. Sekä visuaalis-spatiaalisen että fonologisen kapasiteetin kehittyminen riippuu kuitenkin todennäköisesti keskusyksikkötoimintojen kehittymisestä (Gathercole, ym., 2004).

Tutkimukset osoittavat, että työmuistiresursseja voidaan parantaa harjoittelemalla (Dahlin, Nyberg, Bäckman & Neely, 2008; Turley-Ames & Whitfield, 2003). Säännöllisellä työmuistin harjoittamisella voidaan saada hyviä ja pitkäkestoisia tuloksia (Dahlin ym., 2008), mutta toistaiseksi on olemassa hyvin vähän tutkittua tietoa siitä, parantaako työmuistiresurssien kehittyminen myös oppimista.

Työmuisti ja matematiikka

Työmuistiresursseja tarvitaan kaikissa matemaattisten tehtävien suorittamisen eri vaiheissa (ongelman hahmottaminen, ongelman arviointi, informaation haku säilömuistista, vastauksen laskeminen, varsinainen vastaaminen) (ks. Imbo & Vandierendonck, 2007). Toisaalta eri tehtävätyypit kuormittavat työmuistin komponentteja eri tavoin. Esimerkiksi yksi- ja kaksinumeroisilla luvuilla suoritettavista päässälaskuista on osoitettu, että jopa laskujen esittämistapa vaikuttaa ratkaisemisessa käytettävien resurssien valintaan: peräkkäin kirjoitetut luvut houkuttelevat fonologisten resurssien käyttöön ja päällekkäin kirjoitetut luvut puolestaan visuaalis-spatiaalisten resurssien käyttöön (Trbovich & Le Fevre, 2003).

Keskusyksikkö on työmuistin aivot. Baddeleyn (1986, 1997) näkemyksen mukaan muut järjestelmät ovat pelkkiä varastoja, joissa ei sinänsä voi tapahtua mitään ilman keskusyksikön apua. Keskusyksikkö kontrolloi apujärjestelmiensä toimintaa ja hyödyntää kulloisessakin tilanteessa sopivinta. Keskusyksikön ajatellaan olevan merkittävässä asemassa ongelmanratkaisuprosesseissa ja päätöksenteossa (Baddeley, 1986; Baddeley & Logie, 1999; Logie, 1993; Swanson & Beebe-Frankenberger, 2004). On siis hyvin todennäköistä, että keskusyksikkötoiminnot ovat hyvin olennaisessa osassa myös matemaattisia tehtäviä suoritettaessa.

Fonologista silmukkaa on osoitettu tarvittavan mm. lukumäärän laskemiseen (counting) (Healy & Nairne, 1985; Logie & Baddeley, 1987) sekä kertolaskuihin (Lee & Kang, 2002). On todennäköistä, että sitä tarvitaan juuri monissa sellaisissa toiminnoissa, joissa laskeminen perustuu auditiivis-fonologisesti koodattuun informaatioon (esimerkiksi kertolaskurimpsut).

Visuaalista työmuistia puolestaan on ehdotettu mentaaliseksi työtilaksi, jossa tietynlaisia matemaattisia tehtäviä ratkaistaan ja niissä tarvittavia tietoja säilytetään ja käsitellään. Lisäksi vahvasti visuaalis-spatiaalisten elementtien, kuten geometristen kuvioiden käsittelyn lisäksi on mm. paikka-arvon ymmärtämisen havaittu vaativan visuaalis-spatiaalista hahmottamiskykyä.

Eri-ikäiset hyödyntävät matemaattisten tehtävien ratkaisemisessa eri työmuistikomponentteja. Pienet lapset käyttävät tehtäviä suorittaessaan hyvin voimakkaasti visuaalis-spatiaalisia resursseja. Iän myötä ihmiset hyödyntävät yhä enemmän fonologista työmuistia ja osaavat käyttää paremmin joko visuaalis-spatiaalisia tai fonologisia resursseja tai molempia yhtäaikaisesti (Holmes & Adams, 2006).

Työmuisti ja matematiikan oppimisvaikeudet

Työmuistin ja matematiikan välisiä yhteyksiä on tutkittu kasvavalla tahdilla läpi 2000-luvun. Tutkimukset ovat osoittaneet, että työmuistin kaltaista tiedonkäsittelyjärjestelmää tarvitaan matematiikassa, mutta tarvittavien resurssien luonne vaihtelee mm. tehtävän suorittamisen vaiheen ja tehtävätyypin mukaan. Sekä alle kouluikäisillä (Kyttälä, 2008) että alakouluikäisillä (Andersson & Lyxell, 2007; Geary, Hoard, Byrd-Craven, Nugent & Numtee, 2007; Swanson & Jerman, 2006) matemaattisesti heikoilla lapsilla on usein huono työmuisti. Toisaalta kaikilla lapsilla, joilla on matematiikan oppimisvaikeuksia, ei kuitenkaan ole heikkoa työmuistia.

Matemaattisilta taidoiltaan heikkojen lasten ja nuorten työmuisti on usein heikko vain osittain; he selviävät joistakin työmuistitehtävistä hyvin ja toisista huonosti. Heikkoudet saattavat rajoittua joko fonologisen tai visuaalis-spatiaalisen järjestelmän puolelle, mutta ne voivat ilmetä molemmissa. Se, miten matemaattisilta taidoiltaan heikkojen lasten työmuisti eroaa normaalisti suoriutuvista lapsista, on jossain määrin yhteydessä kielellisiin taitoihin. Se kertoo vaikeuksien kasautumisesta: jos lapsella on sekä matemaattisia että kielellisiä vaikeuksia, hänellä on usein myös laajempia heikkouksia työmuistissa.

Työmuistin tukeminen

Tutkimukset osoittavat, että työmuistia voidaan parantaa harjoittelemalla. Toistaiseksi ei kuitenkaan ole järjestelmällisesti tutkittu, voidaanko työmuistia harjoittamalla parantaa myös oppimistuloksia. Työmuistin kuormitusta voidaan kuitenkin vähentää; keinoina ovat työmuistin toiminnan ”ulkoistaminen” sekä kerralla käsiteltäväksi tulevan tietomäärän rajoittaminen. Yksinkertaisin ratkaisu käytännön koulutyössä on korvata puuttuva muistitila konkreettisilla apuvälineillä, kuten kynällä ja paperilla. Tehtävän olennaiset osat ja niiden suhteet voidaan piirtää näkyviin, ja opetuksessa voidaan rohkeammin soveltaa konkreettisia apuvälineitä sen sijaan, että tukeudutaan voimakkaasti pelkästään symboliseen matematiikkaan. Monimutkaiset tehtävät ja ohjeet voidaan pilkkoa pienempiin palasiin ja välivaiheet merkitä visuaalisesti näkyviin. Tehtävien ja ohjeiden toistaminen on myös tärkeää.

Työmuistin tukemiskeinot riippuvat luonnollisesti jossain määrin lapsen heikoista alueista. Jos auditiivis-fonologinen järjestelmä on heikko, kannattaa kiinnittää erityistä huomiota tehtävien ja ohjeiden pilkkomiseen ja toistamiseen. Auditiivis-fonologisen järjestelmän heikkouksia voidaan myös joskus yrittää kiertää hyödyntämällä visuaalis-spatiaalista järjestelmää esimerkiksi piirtämällä tai käyttämällä muita visuaalis-spatiaalisia apuvälineitä. Konkreettisia apuvälineitä tarvitaan myös työmuistin laajentamiseen silloin, kun visuaalis-spatiaalinen työmuisti on heikko.