Aritmetiska grundfärdigheter
Addition
I finska matematikböcker undervisas addition (med talen 1-9) för närvarande huvudsakligen genom så kallad faktoruppdelning. När man lär sig t.ex. talet sex ska man öva sig alla aritmetiska kombinationer angående talet, såsom 0+6, 1+5, 2+4, 3+2, 4+2, 5+1 och 6+0. Att lära sig enstaka räkneuppgifter är utmanande speciellt för ett barn som har svaga färdigheter och som hittar inga fästpunkter för andra talen, utan ser alla räkneuppgifter som fristående. Räkningen sker långsamt om barnet beräknar bara genom uppräkning. I de senaste forskningarna uppmuntras det att speciellt för de svagpresterande barn, undervisa sådana räknestrategier, som barnet själv inte alltid uppfattar. Genom att undervisa räknestrategier försöker man att förminska information som måste läras utantill. Med hjälp av räkneuppgifter som redan finns i minnet kan man lära sig att lösa sådana räkningar som verkar svåra att minnas. Så kan man också minimera räkningen genom uppräkning. I övningen används konkret och visuellt material och barnet får genom diskussion hjälp att hitta samband mellan räkningar. Räkningarna kan intensifieras t.ex. genom olika spel. Automatiserade räkningar försöks överföra till större talområden genom analogier (t.ex. 2 + 3, 20 + 30). I övningar betonas förståelsen i stället för att räkna upp mekaniskt eller lära sig utantill.
Med hjälp av modellen nedan kan man undervisa räknestrategier för ett barn som har svårigheter att minnas de enklaste additioner inom talområdet 0-20. Modellen kan tillämpas också för hela undervisningsgruppen. Modellen och övningarna baserar sig på rehabiliterings- och/eller undervisningsmetoden utvecklat i Finland (Koponen 2007,2008; Koponen & Mononen 2009) och följande litteratur: Cotter 2007, Haylock & Cockburn 2008, Koponen, Aro & Ahonen 2009 sekä Wright, Martland, Stafford & Stanger 2006.
Vilka räkningar barnet redan behärskar?
När man börjar öva addition med barnet måste man ta reda på hurdana räkneuppgifter barnet redan kan. Detta kan förklaras t.ex. med hjälp av additionskort samt additionstabellen. (Ladda ner tabellen och kort för utskrift, pdf.) Bedömningen kan förverkligas spellik. Läraren eller barnet lägger ett kort åt gången på bordet. Om barnet kan snabbt (under 3-4 sekunder) svara på räkneuppgiften som kortet visar, får han/hon kortet för sig själv. De räkneuppgifter som barnet inte kan, läggs till en annan kortlek. De räkningar som barnet kan svara ringas in i tabellen. Utgående från tabellen börjar man undervisa de räkneuppgifter som barnet inte behärskat. Det centrala är att hitta regelmässighet från räkneuppgifternas strukturer och hjälpa barnet att uppfatta hur kunskap om talradet och begreppet tal fungerar som stöd för räkningen. Å andra sidan övar man sig vissa, så kallade ankareräkningar (t.ex. dubbel och tiopar) och med hjälp av dem övar man beräkna andra räkneuppgifter. I fortsättningen kan man med hjälp av räknekort bedöma om barnet har lärt de räkningar som övat. Då ringar man också in i tabellen de räkningar som barnet redan behärskar. Så här lär barnet veta vad som han/hon redan kan och vilka räkneuppgifter måste ännu övas.
-
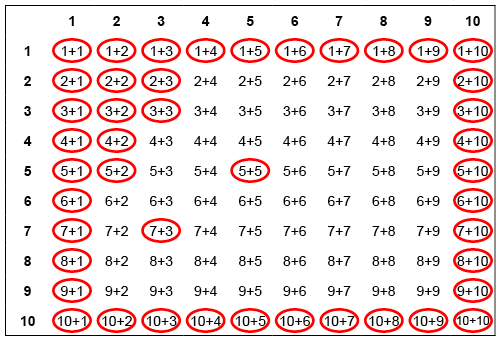
- Ett exempel på en tabell där additioner som barnet behärskar är markerade.
Undervisningsordning för strategier
I det följande finns en modell av undervisningsordning som syftar till att beakta räkningarnas svårighetsgrad vid inlärning och samband mellan räkningar. Barn lär sig alltid att räkna individuellt. Det är möjligt att barnet kan göra enstaka räkneuppgifter men han/hon kan inte göra räkneuppgifter som presenterats tidigare i listan. För att lösa några räkneuppgifter kan barnet använda olika strategier och välja den som passar henne/honom bäst.
|
Räknetyp |
Övning/Bakomliggande tanke |
|---|---|
|
1) Tal + 1 -räkningar |
begreppet tal / talrad + visuellt stöd |
|
2) Tal + 2 -räkningar |
talrad / begreppen jämnt och ojämnt tal + visuellt stöd |
|
3) Fem + tal 1–5 -räkningar |
talbegreppen 6-10 + visuellt stöd |
|
4) Räkningar med tiopar |
ankareräkningar |
|
5) Tioparens närräkningar |
slutledning med hjälp av tiopar |
|
6) 10+ tal -räkningar |
talbegreppen 11-20 |
|
7) Räkningar med talen 5 - 9 |
talen som disponerats via 5 |
|
8) Dubbelräkningar |
ankareräkningar: talradet + regel + visuellt stöd |
|
9) Närdubbelräkningar |
slutledning med hjälp av dubbelräkning |
|
10) 9- och 8 -räkningar |
slutledning med hjälp av 10-räkning |
|
11) Förstärkning av alla räkningar |
övning med hjälp av olika spel och uppgifter |
För varje uppgiftstyp ges exempelövningar. Det centrala i övningen är växelverkan och diskussion mellan läraren och barnet. Genom att fråga och lyssna på barnets lösningsmodeller och matematiskt tänkande kan läraren leda inlärningen framåt och försäkra sig att barnet förstår det som lärs.
Tal + 1 –räkningar
När man adderar ett till talet får man det följande talet. Om barnet inte vet hur mycket är 2 + 1 eller 4 + 1, är det bra att kontrollera om barnet kan säga det följande talet i talradet inom talområdet 1-10 eller om barnet kan berätta svaret till en motsvarande räkneuppgift i en konkret situation (t.ex. ”Hur många äpplen finns det i påsen när det i början fanns 4 och man lade 1 till?”). Om de konkreta situationerna lyckas, ska man först öva talradet och förstärkning av begreppet tal och dess samband med räkningen, dvs. begreppet addition ska klargöras.
Som hjälp vid konkretiseringen kan man använda t.ex. räkneskivor och talföljd. Med hjälp av konkret material kan man också konkretisera bytesprincipen; t.ex. 5 + 1 = 6 ja 1 + 5 = 6. Man kan be barnet att tänka vilken av uppgifterna är lättare att räkna. Tillsammans med barnet konkretiseras hur siffrorna kan byta plats sinsemellan i addition.
Tal + 2 –räkningar
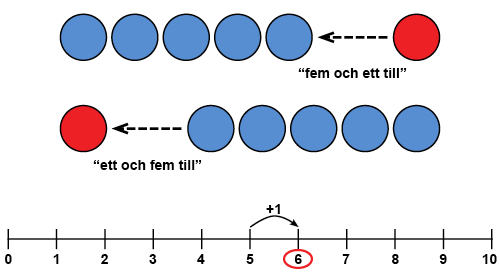
Tal + 2 –räkningar baserar sig främst på att behärska talradet. Om barnet kan berätta vilket tal som kommer efter två steg från ett givet tal eller räkna upp talen med två steg i taget, har barnet ett redskap genom vilket han/hon kan klara av tal + 2 –räkningar. Då behövs förstärkning för samband mellan symboliskt presenterad räkning och rörelse på talradet.
Som stöd för att röra sig längs talraden kan man ta begreppen jämnt och ojämnt tal. Med hjälp av räkneskivor kan talen utformas så att skivorna ordnas under varandra två i bredd (se bild). Barnet kan flytta sina fingrar på skivor (pekfingret och långfingret samtidigt på skivan) och känna hur jämna och ojämna tal känns olika när uppräknandet tagit slut.
Skivor kan i början räknas så att alla skivor räknas en i taget genom att betona jämna tal och slutligen genom att räkna skivor två i taget. När man adderar två till det ojämna talet får man det följande ojämna talet som svar.
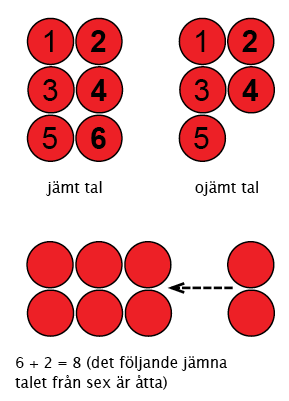
Som stöd för talradsövningen kan man med små barn använda Nalleramsan (Ladda ner Nalleramsan, pdf på finska). I ramsan kan man betona jämna tal. Man kan också räkna upp talradet till tio i två grupper så att den ena gruppen säger tyst de ojämna talen och den andra gruppen lite högre de jämna talen. Slutligen kan man räkna upp bara jämna eller ojämna tal (t.ex. 2, 4, 6, 8 osv.). När barnet behärskar de jämna och ojämna talen är det lättare att addera två till talet.
Fem + tal 1–5 -räkningar
Talen 6–10 kan undervisas redan i början via fem då man också blir bekant med fem + tal 1–5 -räkningar. Förmågan att indela talen 6–10 via fem kan utnyttjas senare då addenderna är lika stora eller större än fem (se även punkten Räkningar med talen 5-9). Räkningarna 5 + 1, 5 + 2, 5 + 3, 5 + 4 ja 5 + 5 kan väl konkretiseras med fingrar eller tvåfärgade räkneskivor. Genom att visa med fingrar, är talet 5 alltid den vänstra handen och med den högra adderar man fingrar vid behov. Antalen 5 + tal 1–5 kan i början avbildas med fingrar och be barnet att visa dem på samma sätt. ”Lyfta fem fingrar på din andra hand; lyfta ett finger på den andra handen; titta på dina fingrar och berätta hur många fingrar har lyfts?” Med små barn kan man också öva att visa talen från fingrar med hjälp av ramsan (ladda ner och skriv ut Nalles tiorap, pdf på finska).

Räkningar med tiopar
Tioparen betyder räkningar där addendernas summa är jämnt tio (t.ex. 4 + 6). Att behärska tioparen bra hjälper barnet t.ex. i tioparens närräkningar (såsom 4 + 5) samt i räkningar där addend är 8 eller 9.
Att öva tioparen är bra att börja konkret genom att dela 10 saker för två, på olika sätt. Som medlen i uppgiften kan man använda t.ex. räkneskivor. Man kan t.ex. dela 10 hundkex för två hundar samt 10 karameller eller 10 euro mynt för två barn. Olika delningar kan antecknas t.ex. genom att rita eller skriva på papper.
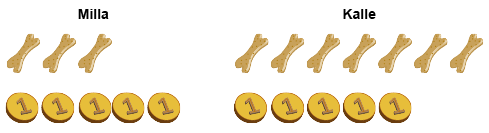
Slutligen kan olika kombinationer ordnas så att enhetlighet i räkneuppgifterna dyker upp.
| 0 + 10 |
| 1 + 9 |
| 2 + 8 |
| 3 + 7 |
| 4 + 6 |
| 5 + 5 |
| 6 + 4 |
| 7 + 3 |
| 8 + 2 |
| 9 + 1 |
| 10 + 0 |
För det andra kan man öva igenkänna det återstående antalet, t.ex. hur mycket fattas till talet tio. Detta kan man öva t.ex. med fingrar, räkneskivor eller med hjälp av kortspel. Man kan lyfta en viss mängd fingrar upp och fråga hur många som finns nere (t.ex. 2 uppe och 8 nere). Om man använder räkneskivor kan en del av räkneskivorna gömmas under burken eller handen och sen fråga barnet hur många räkneskivor som finns undangömda. Så att uppgiften fokuserar sig på att öva tioparen är det viktigt att gruppera räkneskivor i grupper om fem. Så blir det snabbare för barnet att uppfatta det synliga antalet. Skivorna kan även användas som kort då 0-10 skivor finns synliga och barnets uppgift är att säga hur många som fattas till tio skivor. Du kan ladda ner och skriva ut antalskort här.

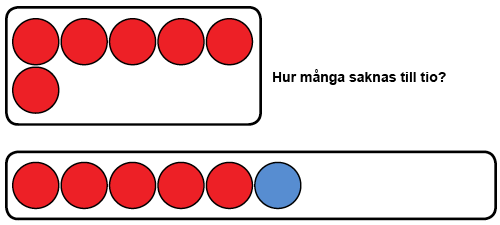
Spelandet motiverar ofta barn att upprepa räkningar som håller på att läras eftersom varje spel är alltid annorlunda. Kaatisspel är ett spel om tioparen för 2-4 spelare. För att spela spelet behövs sex serier korten 1–9 (tillsammans 54 kort) antingen av vanliga spelkort, eller du kan ladda spelkorten ner och skriva ut här. Här kan du också ladda ner och skriva ut regler till Kaatisspelet. Spelkorten kan användas också till andra spelen som presenteras på denna webbplats.
Med tanke på datorstödd träning kan man hitta övningar om tioparen bl.a. i programmet Neure-Express i avsnittet additioner.
Tioparens närräkningar
Räkningar där den andra av addenderna är ett större eller mindre än den andra av faktorerna i tioparsräkningen, kallas för tioparens närräkning (t.ex. tioparens 7 + 3 närräkningar är 7 + 4, 4 + 7, 7 + 2 och 2 + 7). För att lösa räkningar kan man använda inlärda tioparen som hjälp. I övningarna bildar man först ett tiopar. Efter detta adderas eller subtraheras ett då man får räkningen som håller på att läras. Det är viktigt att diskutera med barnet så länge att han/hon märker sambandet mellan de två räkningarna. Barnet kan uppfatta att angående tioparsräkningar där den andra faktorn är ett större än den andra, blir svaret alltid 11. Som en övningsuppgift kan barnet bes att hitta på räkningar där svaret är 11.
10+ tal -räkningar
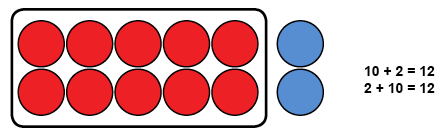
Talen 11–19 formas av tior och ettor. Kunskap om detta att t.ex. talet 15 är 10 + 5 kan barnet utnyttja t.ex. i räkneuppgifter som innehåller talen 8 eller 9. Barnet kan först fundera vad svaret skulle vara om talen 8 och 9 ersatte med 10 (se även 9- och 8-räkningar). När man konkretiserar 10 –räkningar är det bra att påminna barnet om bytesprincipen: Addendernas räkningsordning spelar ingen roll med tanke på svaret. Barnet kan ändra addendernas ordning till den som verkar mer bekant.
I räkneskivor håller man tiotalet hela tiden orörd medan antalet ettor ska bytas. Barnet kan bes nämna och/eller skriva en räkning eller bilda den enligt skriven eller utsagt form. Tio räkneskivor kan fästas på pappret med häftmassa då man kan lätt röra dem när man bildar räkningar eller adderar tio till ett tal (t.ex. 3 + 10).
Räkningar med talen 5 - 9
När barnet kan indela talen 6–10 via fem kan han/hon utnyttja detta med alla räkningar där addenderna är mellan 5-9. Räkningarna kan konkretiseras med hjälp av räkneskivor samt med fingrar. En exempelräkning 6 + 7 kan konkretiseras med tvåfärgade räkneskivor via grupper om fem (se bilden nedan). Barnet kan lätt iaktta två grupper om fem som formas talet tio. Således blir det kvar räkningen 1 + 2 som barnet uppfattar att bilda summan 3. När räkningarna kombineras blir det 10 + 3 som barnet har lärt sig tidigare och vet svaret vara 13.
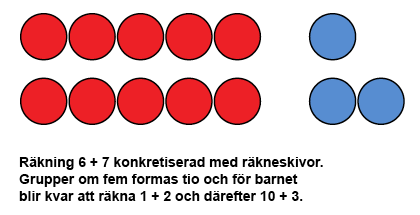
När man konkretiserar med fingrar vet barnet att talet 6 är 5 och 1. Således lyfter barnet upp bara ett finger och lägger fem på minnet. Talet 7 består däremot av 5 och 2 då barnet lyfter två fingrar på andra handen och lägger fem på minnet. De båda femmorna finns på minnet och utformar tio. Barnet lägger ihop 2 och 1, adderar svaret tre till tio som finns på sitt minne och får svaret 13.
Dubbelräkningar
Dubbelräkningar eller dubbel kallas för räkningar där de båda addenderna är desamma (t.ex.6 + 6). Svaret till räkningar är alltid ett jämnt tal. I början kan man öva små dubbelräkningar, alltså de räkningar där summan är tio eller mindre. Som hjälp i konkretisering av räkningarna kan man använda fingrar (små dubbel), räkneskivor och t.ex. spegel samt kombinera räkningarna till dubbel som finns i omgivningen (t.ex. bilens fram- och bakdäck 2 + 2 = 4, myrans fötter 3 + 3 = 6, spindels fötter 4 + 4 = 8 osv.) När man övar små dubbel kan man be barnet att lyfta t.ex. två fingrar på ena handen och två fingrar på andra handen och berätta svaret. Uppgiften kan göras först så att fingrarna syns och sen så att fingrarna läggs på huvudet som ”kaninöron”. Antalen kan fördubblas även med hjälp av en spegel. När man sätter tre räkneskivor framför spegeln, fördubblar den antalet då det finns 3 och 3 räkneskivor, alltså 6. Som stöd för spegelövningen kan du ladda ner och skriva ut dubbelramsan (på finska).

Med räkneskivor kan man öva dubblering så att läraren lägger först ett antal räkneskivor på bordet och barnet fördubblar det. Om man använder två färger är det lättare för barnet att märka en grupp om tio. När barnet först har övat dubblering genom att öka skivor kan man försöka göra så att barnet bara säger svaret till talet som läraren byggt eller sagt.
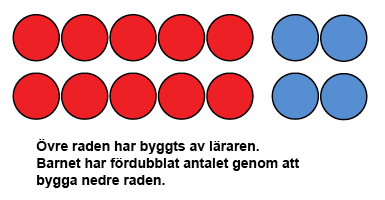
Dubblering kan även övas så att dubbelmängden varierar och barnet ska hitta på räkningar av dem. Det är viktigt att inse att skillnaden mellan två bredvidliggande dubbel är alltid två.
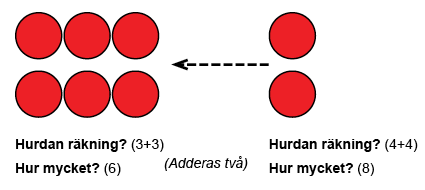
Datorstödda dubbleringsövningar finns bl.a. i additionsdelen av Neure-Express.
Närdubbelräkningar
För närdubbelräkningar kallar man räkningar där addenderna kommer efter varandra i talraden. Som stöd för att lösa räkneuppgifter kan man använda de tidigare inlärda dubbelräkningarna. I övningarna bilder man först en dubbelräkning och sen adderar eller subtraherar ett då man får räkningen som håller på att läras. Det är viktigt att diskutera med barnet så länge att han/hon uppfattar sambandet mellan de två räkningarna. I närdubbelräkningar kan barnet utnyttja dubbelräkningen som formas av en mindre addend (t.ex. räkningen 5 + 6 kan lösas med hjälp av räkningen 5 + 5) och addera ett till svaret. Räkningen 5 + 6 kan lösas också med hjälp av räkningen 6 + 6 men då måste man subtrahera ett från svaret. Utöver räkneskivor kan man öva liten dubbels närdubbelräkningar med fingrar. Barnet lägger fingrarna på huvudet som ”kaninöron”. Läraren säger: ”Visa två och två med fingrar. Hur mycket är det tillsammans? Lyfta ett finger till på andra handen. Vilka tal har du nu? Hur mycket är det tillsammans?”
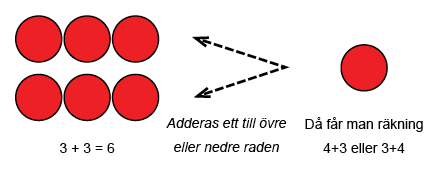
Det mest utmanande för barnet är att lära vilken av alla inlärda räkningarna ska användas som hjälp vid lösningen av sådana räkningar som inte ännu har automatiserats. För att välja hjälpräkningen kan barnet prova en övning: efter att ha löst räkningen ska barnet tänka om han/hon har kommit ihåg räkningen utantill och vilken hjälpräkning han/hon använde vid behov. På bilden nedan finns det ett exempel på övningen som finns på papper.

(Koponen 2008)
9- och 8 -räkningar
Räkningar där addenderna är 9 eller 8 kan jämföras med tioräkningar (t.ex. 10 + 3). Dessutom kan de tidigare inlärda tioparen utnyttjas vid räkningen (t.ex. 8 + 2). Det finns två sätt att närma sig räkningarna.
För det första kan man ta upp två räkningar som jämförs. T.ex. hur skiljer sig 10 + 5 från 9 + 5? Frågan konkretiseras t.ex. med räkneskivor. Eftersom nio är ett mindre än tio kan räkningen först tänkas som en tioräkning och subtrahera ett från summan (9 + 5 = 10 + 5 - 1). I räkningen 8 + 7 är åtta två tal mindre än tio så att med tanke på tioräkningen måste man subtrahera två från summan (t.ex. 8 + 7 = 10 + 7 - 2).
För det andra kan man komplettera 9- och 8 -räkningar till tio. Först granskas vad som är skillnaden mellan talen 9 och 10 (1). T.ex. i räkningen 9 + 4 ges ett tal från fyra till nio vilket kompletterar den som tio. Det blir en mellanräkning 10 + 3 som barnet har redan tidigare lärt. I räkningar där den andra av addenderna är 8 märks det att när man kompletterar till tio måste man ge två bort från den andra addenden.
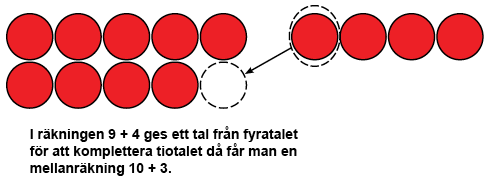
Förstärkning av alla räkningar
De inlärda räkningarna kan förstärkas med hjälp av kortspel. Räkningarna i varje spel är olika, vilket motiverar barnet att spela allt mer. Additionskrigsspelet är ett spel för två spelare. Det finns två versioner av spelet: talområdet i det ena spelet är 1–10 och i det andra 1–20. Här kan du ladda ner och skriva ut spelanvisningar. Vanliga spelkort (korten 1–9, sammanlagt 36 stycke) passar bra eller du kan ladda ner och skriva ut spelkorten här. Korten kan skrivas ut på färgat papper, klippas och lamineras.
Subtraktion
I finska matematikböcker undervisas subtraktion relativt jämsides med addition. I några material undervisas både additioner och subtraktioner genom så kallad faktoruppdelning. När man lär t.ex. talet sex ska man öva sig alla aritmetiska kombinationer angående talet, såsom 0+6, 1+5, 2+4, 3+2, 4+2, 5+1 och 6+0. Dessutom kan man lära sig även räkningarna 6 – 0, 6 – 1, 6 – 2, 6 – 3, 6 – 4, 6 - 5 ja 6 - 6. Det är viktigt att barnet inser sambandet mellan två delar och en helhet (t.ex. av talen 1, 4 och 5 får man fyra olika räkningar: 1 + 4 = 5, 4 + 1 = 5, 5 - 1 = 4 ja 5 – 4 = 1). Behärskning av additioner kan hjälpa vid inlärningen av subtraktioner när deras samband presenteras för barnet.
Inom talområdet 0 – 20 kan flera olika subtraktioner utföras. Räkningen sker långsamt om barnet beräknar bara genom uppräkning. I de senaste forskningarna uppmuntras det att speciellt för de svagpresterande barnen, undervisa sådana räknestrategier, som barnet själv inte alltid uppfattar. Genom att undervisa räknestrategier försöker man att förminska information som måste läras utantill. Med hjälp av räkneuppgifter som redan finns i minnet kan man lära sig att lösa sådana räkningar som verkar svåra att minnas. Så kan man också minimera räkningen genom uppräkning. I övningen används konkret och visuellt material och barnet får genom diskussion hjälp att hitta samband mellan räkningar. Räkningarna kan intensifieras t.ex. genom olika spel. Automatiserade räkningar försöks överföra till större talområden genom analogier (t.ex. 5 - 4, 50 - 40). I övningar betonas förståelsen i stället för att räkna upp mekaniskt eller lära sig utantill.
I det följande presenteras en modell av hur undervisning av räknestrategier kan framskridas när barnet har svårigheter att lära sig addition och subtraktion inom talområdet 0-20. Modellen kan tillämpas också för hela undervisningsgruppen. Modellen och övningarna baserar sig på rehabiliterings- och/eller undervisningsmetoden utvecklat i Finland (Koponen 2007,2008; Koponen & Mononen 2009) och följande litteratur: Cotter 2007, Haylock & Cockburn 2008, Koponen, Aro & Ahonen 2009 sekä Wright, Martland, Stafford & Stanger 2006.
Vilka räkningar barnet redan behärskar?
När man börjar öva subtraktion med barnet måste man ta reda på hurdana räkneuppgifter barnet redan kan. Detta kan förklaras t.ex. med hjälp av subtraktionskort samt subtraktionstabellen. (Ladda ner tabellen och kort för utskrift, pdf.) Bedömningen kan förverkligas spellik. Läraren eller barnet lägger ett kort åt gången på bordet. Om barnet kan snabbt (under 3-4 sekunder) svara på räkneuppgiften som kortet visar, får han/hon kortet för sig själv. De räkneuppgifter som barnet inte kan, läggs till en annan kortlek. De räkningar som barnet kan svara ringas in i tabellen. Utgående från tabellen börjar man undervisa de räkneuppgifter som barnet inte behärskat. Det centrala är att hitta regelmässighet från räkneuppgifternas strukturer och hjälpa barnet att uppfatta hur behärskning av addition samt kunskap om talradet och begreppet tal fungerar som stöd för räkningen. I fortsättningen kan man med hjälp av räknekort bedöma om barnet har lärt de räkningar som övat. Då ringar man också in i tabellen de räkningar som barnet redan behärskar. Så här lär barnet veta vad som han/hon redan kan och vilka räkneuppgifter måste ännu övas.
-

- Ett exempel på en tabell där subtraktioner som barnet behärskar är markerade.
Förståelse för sambandet mellan addition och subtraktion
Om barnet uppfattar sambandet mellan addition och subtraktion, förminskas mängden av räkningarna som måste inläras. När barnet lär sig att skapa anknytningar mellan tre tal – två delar och en helhet – kan han/hon göra fyra olika räkningar med tre tal. Sambandet kan klargöras med hjälp av en cirkelfigur där det förekommer delar och helheter. Denna figur kan användas i vilket skede som helst vid inlärning av addition och subtraktion. En del-helhet-cirkelfigur kan även utnyttjas vid lösandet av enfasiga verbala uppgifter. Då placerar barnet talen ifråga in i rätta cirklar och tänker på vilka av räkneuppgifterna ska användas. Cirkelfiguren kan tillämpas också senare med multiplikation och division. I förskoleskedet, innan man börjar skriva siffror in i cirklar, kan t.ex. olika föremål (pinnar, räkneskivor osv.) användas.


I sådana subtraktioner där räkningens minuend och subtrahend ligger nära varandra kan man använda addition som en strategi. Räkningen kan ske genom att räkna upp talen en i taget från subtrahend till minuend (t.ex. 8 – 6 kan tänkas som 6…7, 8). Barnet kan även använda talen 5 och 10 som stödjepunkter. Om subtrahend är mindre än fem (t.ex. 7 – 4) kan den först kompletteras till fem (1), och sen adderas ett nödvändigt tal så att minuenden (7) nås. Talen som adderats, alltså 1 och 2, läggs ihop då får man svaret 3. Att komplettera till fem är en fördel om barnet har lärt sig talen 6–10 via fem (t.ex. sju är fem och två). När minuend är större än tio kan subtrahend först kompletteras till tio och sen addera minuendens ettor till talet. T.ex. i räkningen 13 – 8 kan åttan först kompletteras till tio genom att addera två. När barnet vet att 13 är 10 och 3 adderar han/hon de tre som blivit kvar från tio, till två och får svaret fem.
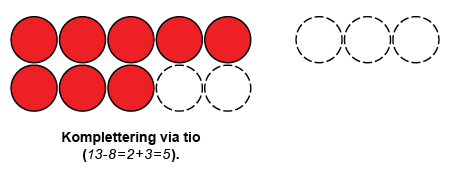
Undervisningsordning för strategier
I det följande har det presenterats en möjlig undervisningsordning där man har strävat efter att beakta svårighetsgraden vid inlärning av räkningar samt räkningarnas samband mellan varandra. Barnen lär sig kunskaper vanligen i olika takt. Det är möjligt att fast barnet behärskar några räkningar kan han/hon inte göra räkneuppgifter som presenterats tidigare i listan. För att lösa några räkningar kan man använda flera olika strategier, av vilka barnet kan välja den som passar honom/henne bäst.
|
Räkningstyp |
Övning/bakomliggande tanke |
|---|---|
|
1) Subtrahera två samma tal från varandra |
Begreppet tal/begreppet subtraktion |
|
2) Subtrahera ett-räkningar |
Begreppet tal/talrad+ visuellt stöd |
|
3) Subtrahera två- räkningar |
talrad/begreppen jämnt och ojämnt tal +visuellt stöd |
|
4) Subtrahera på varandra följande tal från varandra |
begreppet tal/talrad+visuellt stöd |
|
5) Subtrahera från tio |
Slutledning med hjälp av tioparen |
|
6) Subtrahera från talen 9 och 11 |
Slutledning med hjälp av tioparen och 10-x räkning |
|
7) Subtrahera tio från ett tal |
Begreppen av talen11-20 |
|
8) Subtrahera talen 8 och 9 via tioräkning |
Slutledning med hjälp av 10-x räkning |
|
9) Dubbel och närdubbel |
Samband mellan subtraktion och addition |
|
10) Förstärkning av alla räkningar |
Övning med hjälp av olika spel och uppgifter |
För varje uppgiftstyp ges exempelövningar. Det centrala i övningen är växelverkan och diskussion mellan läraren och barnet. Genom att fråga och lyssna på barnets lösningsmodeller och matematiskt tänkande kan läraren leda inlärningen framåt och försäkra sig att barnet förstår det som lärs.
Subtrahera två samma tal från varandra
När två samma tal subtraheras från varandra är skillnaden alltid nolla. Detta kan konkretiseras genom att ge barnet några räkningar att räkna med hjälp av fingrar eller räkneskivor (såsom 5 – 5, 3 – 3, 6 – 6) och fråga barnet om han/hon märker någon regel i räkningarna. Det lönar sig att skriva räkningarna upp. Efter detta kan man prova detsamma med några större tal (såsom 12 – 12 eller 20 – 20).
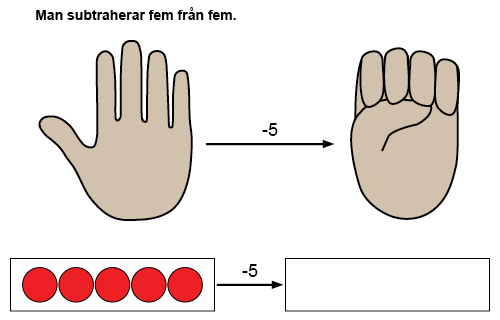
Subtrahera ett-räkningar
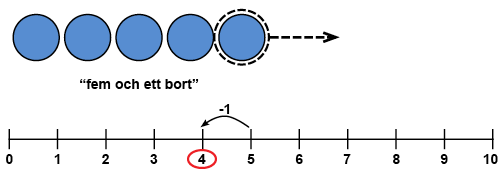
När man subtraherar ett från ett tal får man det föregående talet som svar. Detta kan konkretiseras t.ex. med räkneskivor och talradet och genom att fråga det föregående talet i talradet (t.ex. vilket tal som kommer före talet fem?).
Subtrahera två- räkningar
När barnet har övat jämna och ojämna tal i additionsövningar samt att röra med två steg i talradet kan subtraktion med två tal kopplas till tidigare inlärt. När man subtraherar två från ett jämnt tal får man det föregående jämna talet som svar. Med hjälp av räkneskivor kan talen formas så att skivorna ordnas två i bredd (se bilden). Skivorna subtraheras alltid två åt gången.
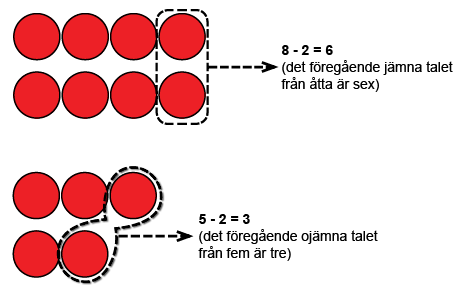
Subtrahera på varandra följande tal från varandra
När två på varandra följande tal (t.ex. 4 och 3) subtraheras från varandra så att det mindre subtraheras från det större talet blir svaret alltid ett. Förhållandet mellan på varandra följande tal kan betraktas t.ex. med hjälp av räkneskivor och talradet. Med räkneskivor betraktas saken genom att sätta två på varandra följande tal under varandra på bordet. Det märks att i det större antalet finns en skiva mer. Om man tog den mindre mängden skivor bort, skulle bara en skiva bli kvar. I talradet kan man betrakta saken genom att söka två vilka som helst på varandra följande tal och titta vad deras avstånd från varandra är.
[KUVA]
Subtrahera från tio
När barnet övar tioparen i additionskedet lär han/hon att känna till räkningens återstående faktorn. I uppgifterna övades hur mycket saknas det från talet tio, eller beräknades hur många räkneskivor som var gömda under burken. Kortspel av tiopar övade också samma sak. Som subtraktion skulle tioparen presenteras t.ex. med räkningen 10 – 6. Om barnet redan behärskar tioparen kan sambandet till subtraktion presenteras t.ex. med hjälp av del-helhet-cirkelfiguren. Om tioparen inte har automatiserats löner det sig att öva dem på nytt i subtraktioner (se mer här).

Subtrahera från talen 9 och 11
När barnet kan subtrahera flytande från tio kan kunskapen utnyttjas även när man subtraherar ett tal från talen 9 eller 11. T.ex. i räkningen 9 - 6 kan tänkas först subtrahera sex från tio då det blir kvar fyra. Eftersom nio är ett mindre än talet tio måste man subtrahera ett till från svaret (9 – 6 = 10 – 6 – 1 = 3). Talet 11 är däremot ett större än talet tio. Om räkningen tänkas först via tio måste man addera ett till svaret, för elva är ett större än tio (t.ex. 11 – 7 = 10 – 7 + 1 = 4).
Det, att i några räkningar man kan använda olika strategier märks t.ex. i räkningen 9 - 5 eller 9 - 4. Barnet kan tänka räkningen via tio såsom ovan men utnyttja kunskapen om att talet nio har lärts via fem. Om barnet har lärt sig att ”nio är fem och fyra” kan han/hon tillämpa kunskapen även i subtraktioner ifråga. Räkningen konkretiseras också klart genom att se efter i fingrar.
Subtrahera tio från ett tal
Barnet har lärt sig att talen 11–19 formas av en tio och ettor. När additioner övades, utformades också dem (t.ex. 10 + 5). När man subtraherar tio från talen 11–19 kan man utnyttja det som barnet redan lärt sig. Saken kan konkretiseras med hjälp av del-helhet-cirkelfiguren där räkningen kan tänkas via addition (hur mycket måste man addera till den synliga delen att man får en helhet).
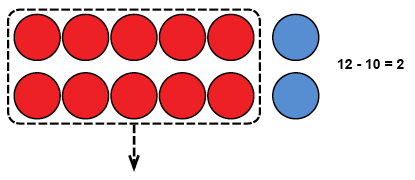
Även räkneskivor passar för att konkretisera räkningar. Det är bra att fästa 10 räkneskivor färdigt på papper med häftmassa då det blir lättare att flytta dem. När man subtraherar tio från ett tal blir alltid ettor kvar.
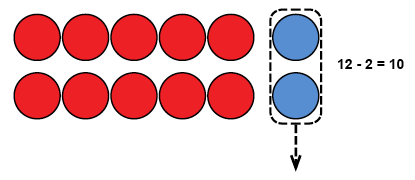
På samma sätt kan man öva subtrahera ettor från ett tvåsiffrigt tal inom talområdet 11–19. T.ex. i räkningen 12 – 2 flyttar man bort två räkneskivor. När man upprepar liknande räkningar märker man att det som blir alltid kvar, är tio, eftersom talen 11–19 består av en tio och en viss mängd ettor.
Subtrahera talen 8 och 9 via tioräkning
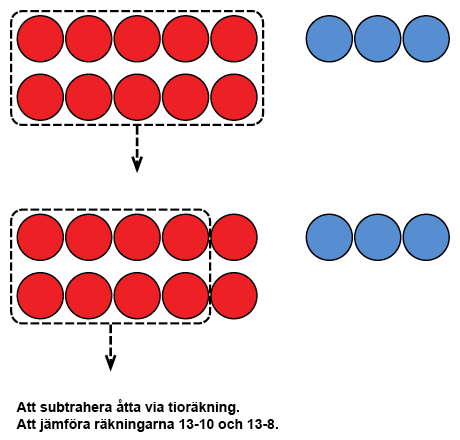
När man subtraherar 8 eller 9 från ett tal kan man använda tioräkning som hjälp. När barnet behärskar räkningar där man subtraherar tio från talen 11–19 (t.ex. 16 – 10) kan han/hon utnyttja kunskapen. T.ex. räkningen 13 – 9 kan först tänkas som 13 – 10 då svaret blir 3. Genom att diskutera med barnet och jämföra räkningarna 13 – 10 och 13 – 9 märks det att 9 är ett mindre än tio så att man måste addera ett till att få svaret. På samma sätt kan man göra när subtrahenden är 8. Då jämförs t.ex. räkningarna 13 – 10 ja 13 – 8 och märks att skillnaden mellan åtta och tio är två som måste adderas till svaret när hjälpräkningen har först räknats 13 – 10 (13 – 8 = 13 – 10 + 2 = 5).
Dubbel och närdubbel
Behärskning av dubbel och närdubbel kan utnyttjas även i subtraktioner. Sambandet mellan subtraktion och addition kan igen visas med del-helhet-cirkelfiguren. I början kan man skriva in i cirkeln bara dubbelräkningens delar av vilka barnet räknar en helhet. Därefter kan man fråga vilken subtraktion barnet får av talen.
På den andra del-helhet-cirkelfiguren kan man skriva en närdubbelräkning. Om barnet kan t.ex. räkningen 12 – 6 kan han/hon utnyttja kunskapen i räkningen 13 – 6 där svaret är ett mer än i dubbelräkningen. ”Att halvera” dubbel vid behov, kan konkretiseras med hjälp av räkneskivor. I början bildar man en dubbelräkning av talet 6: ”6 och 6 är 12”. Samma räkning visas med del-helhet-cirkelfiguren. Då täcker man den andra raden: ”6 av 12 är 6”. Detta visas också med cirkelfiguren.
Förstärka alla räkningar
De inlärda räkningarna kan förstärkas med hjälp av spel. Räkningarna i varje spel är olika, vilket motiverar barnet att spela allt mer. Subtraktionskrigsspelet är ett spel för två spelare. Det finns två versioner av spelet: talområdet i det ena spelet är 1–10 och i det andra 1–20. Här kan du ladda ner och skriva ut spelanvisningar. Vanliga spelkort (korten 1–9, sammanlagt 36 stycke) passar bra eller du kan ladda ner och skriva ut spelkorten här. Korten kan skrivas ut på färgat papper, klippas och lamineras.



