Förståelse av matematiska samband
Förutom goda grundläggande räknefärdigheter utgör behärskning av talsystemet ett annat, mycket centralt kärnområde för matematiska färdigheter hos barn i nybörjarundervisning. För att kunna förstå och skriva tal samt utnyttja denna information i sitt räknande ska barnet lära sig många olika regler och principer för både det muntliga och skriftliga talsystemet. För att kunna förstå talens platsvärde och tiobassystemet ska barnet kunna skapa förbindelser i det nätverk som bildas av talnamn, siffersymboler, konkret material och bilder. Genom att förbinda element från alla dessa fyra delområden med övningar i platsvärde och tiobassystem kan man stödja barnets förståelse för tiobassystemet.
Principer för talens platsvärde och tiobassystemet
I följande avsnitt beskrivs sådana principer som barnet borde förstå om positions- och tiobassystemet (t.ex. Lawton 2006, Haylock & Cockburn 2008).
Platsvärde
Vårt system har bara 10 tecken för siffror (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) med vars hjälp man kan bilda en oändlig mängd av olika tal genom att uttnyttja positionssystemet. Siffrans plats i talet anger dess värde. Platsen längst till höger representerar ental, sedan nästa till vänster står för tiotal, nästa för hundratal och så vidare, alltid tiofaldigt i jämförelse med den föregående platsen. På det sättet t.ex. får siffran 8 i talet 800 ett tiofaldigt värde i jämförelse med dess värde i talet 80.
Enhetsbyte
Tio stycken av samma talenhet kan bytas till en talenhet som står på vänstra sida, och tvärtom kan ett stycke av en talenhet bytas till tio talenheter som står på högra sida. Principen kan klargöras genom konkret material och verbalisering.

”En av dessa är tio stycken av dem.” ”En tiostav är tio enbitar.”
eller
”Tio av dessa är en av dem”. ”Tio enbitar är en tiostav.”
Förståelsen för principen för enhetsbyte samt förmågan att kunna uttnyttja den är viktiga färdigheter då man senare räknar med uppställning. Vid addition ”ger” man de enheter som blir kvar av en talenhet till nästa talenhet till vänster. (T.ex. om summan av entalen 8+4 är 12, lämnar man ental, dvs. 2, i platsen för ental och ger ett tiotal till tiotal som markeras som en minnessiffra ovanpå tiotalen.) Om man däremot subtraherar med uppställning - om det inte finns ett tillräckligt stort tal att subtrahera från - ”lånar” man dvs. man byter en större talenhet till tio mindre. (T.ex. Om man i platsen för ental borde subtrahera 4 med 5, ”lånar” man tio från tiotal som byts till tio ental och läggs till i de ursprungliga entalen, då man kan räkna 14-5). Då får man emellertid inte glömma markera att det nu finns ett tiotal mindre.
Kombinering av konkret material med siffersymboler
Kombinering av konkret material och siffersymboler kan klargöras t.ex. genom att använda färdigt tiobasmaterial eller med gummiband buntade pinnar som kombineras med ett skrivet två- eller tresiffrigt tal (se övningarna nedan).
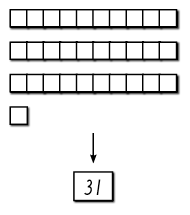
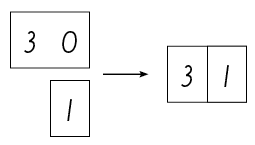
Man kan öva sig att bilda tal med siffersymboler med hjälp av sifferkort som läggs på varandra (ental, tiotal och hundratal). Sifferkorten, som läggs på varandra, klargör vad som händer när man skriver ett tal som består av mer än bara en siffersymbol. På det sättet klargörs den så kallade regeln att skriva på.
Kombinering av talnamn med siffersymboler
Att skriva och säga ett tal går inte alltid hand i hand. T. ex. talet som skrivs 467 sägs ”fyrahundrasextiosju”. Orden ”hundra” och ”tio” syns praktiskt taget inte i det skrivna talet, utan barnet måste veta att nummer 4 står på platsen för hundratal och nummer 6 på platsen för tiotal. När barnet måste skriva talet antingen med hjälp av konkret material eller efter diktamen, förekommer det ofta att barnet försökt skriva talet exempelvis på följande sätt: 400607, 40067 eller 4067. Då kan barnet ännu inte regeln att skriva på och förstår inte platsernas betydelse i talet. Detta kan dock övas med hjälp av konkret material och sifferkort som läggs på varandra och genom att tillfoga verbalisering av talen till övningen (se övningarna nedan).
Noll
Noll uttrycker en tom plats för talenheter. Med hjälp av konkret material kan man klargöra att ett tal inte alltid innehåller alla talenheter och att man då ska skriva en nolla på ”den tomma platsen”. Då man uttalar talnamn hörs nollan inte, vilket gör det krävande för en del barn att skriva tal.
Övningar för förståelse för talens platsvärde och tiobassystemet
I följande avsnitt presenteras några övningsuppgifter som kan användas individuellt med bara ett barn eller i grupp, när man övar på talens platsvärde och tiobassystemet. Övningarna baserar sig på en rehabiliterings- och/eller undervisningsmetod som är utvecklad i Finland (Koponen & Mononen 2009) samt på följande litteratur: Haylock & Cockburn 2008, Wright, Martland, Stafford & Stanger 2006 och Cotter 2007.
Material som används i uppgifterna
| Tiobasmaterial | Material av plast eller träd some innehåller enbitar, tiostavar, hundraplattor och tusenkuber. |
| Pinnar | Med gummiband buntade pinnar, tio pinnar i varje bunt, samt fristående pinnar (t.ex. pysselpinnar). |
| Sifferkort (Ladda ner sifferkort för utskrift här, pdf) |
Siffrorna 1-9 samt tio- och hundratal och ett tusenkort. Korten kan läggas på varandra från höger, så att man får det önskade talet. |
| Hundratavla (Ladda ner hundratavlan för utskrift här, pdf; ladda ner en tom bas för hundratavlan för utskrift här, pdf) |
En tabell med talen 1-100. |
Övningsuppgifter
| Talenheter (pinnar) |
I uppgiften behöver man massor av pinnar, vars antal barnet ska reda ut. Pinnarna är buntade t.ex. med gummmiband, och varje bunt har tio pinnar. Först bestäms hundra pinnar genom att räkna dem i buntar av tio pinnar (10, 20, 30...100). Tio buntar binds ihop med ett gummiband. Till slut räknas antalet pinnar – hundratal, tiotal, ental – och det markeras med siffror. |
| Att bilda tal med sifferkort inom talområdet 1-100 (sifferkort) |
Med hjälp av uppgiften klargörs, hur de siffror som i tvåsiffriga tal står på platsen för ental skiftar i tur och ordning mellan 0 och 9. Efter nian kommer alltid nästa jämna tiotal, där det står en nolla på platsen för ental. Barnet lägger tiotalskort på bordet i en uppställning och bredvid dem entalskort på samma sätt. Läraren börjar räkna upp tal framåt från 1. Efter varje uppräknat tal bildar barnet talet i fråga med sifferkort. I början kan läraren räkna upp tal till 30-40, men som en mer krävande uppgift kan talen uppräknas och bildas ända till 100. |
| Att bilda tal i enlighet med uttrycket (tiobasmaterial, pinnar och sifferkort) |
Läraren säger t.ex. ”34” och barnet bildar talet med hjälp av materialet (tiobasmaterial eller pinnar) eller sifferkort (lägger korten 30 och 4 på varandra). |
| Att bilda tal i enlighet med talet i bilden (tiobasmaterial, pinnar och sifferkort) |
A) Läraren visar t.ex. talet 89 med sifferkort och barnet bildar talet med hjälp av materialet (tiobasmaterial eller pinnar) och säger talet högt. B) Läraren bildar talet med hjälp av materialet och barnet bildar talet med sifferkort och säger det högt. |
| Kan du hitta talet -spel (sifferkort) |
Sifferkorten läggs på bordet i oordning (antingen alla kort, ental och tiotal eller tiotal och hundratal). Läraren säger högt tal som barnet ska bilda på sidan om bordet med hjälp av sifferkort. ”Kan du hitta talet 30?” ”Kan du hitta talet 47?” Barnet har kunnat bilda alla tal rätt om det sistnämnda talet blir kvar. |
| Sifferkort (sifferkort) |
A) Barnet lägger sifferkorten 10-100 i storleksordning, pekar på dem i tur och ordning och säger talen framåt (och ev. bakåt) (10, 20, 30...100). Därefter kan man vända ett kort i talraden och barnet ska nämna det vända kortet. B) Övningen görs på samma sätt som övning A, men med korten 100-1000 (100, 200, 300...1000). |
| Tiotal och ental som inledningstal (tiobasmaterial eller pinnar) |
Inledningstalet är t.ex. 32. Barnet bildar talet och säger det högt. Barnet lägger till en tiostav eller en bunt med tio pinnar alltid när han/hon räknat tio till (32, 42, 53 osv.). |
| Det följande eller föregående jämna tiotalet eller hundratalet (sifferkort) |
A) Tiokorten läggs på bordet i en hög med baksidan upp. Barnet vänder ett kort och säger högt det följande eller det föregående (såsom bestämts) jämna tiotalet (t.ex. barnet vänder kortet med talet 50 och säger sedan talet 60). B) Övningen görs på samma sätt som övning A, men med hundratalskort. Barnet säger högt det följande eller det föregående hundratalet. |
| Vilket tal är gömt? (hundratavlan och den tomma bas för hundratavlan) |
Läraren täcker några tal i hundratavlan med hjälp av t.ex. pappersbitar (t.ex. 5, 25, 75, 85 och 95) och frågar sedan: ”Vilket tal är gömt?” Detsamma kan också göras med hjälp av den tomma hundratavlan. Det är viktigt att fråga barnen hur de löser problemet (dvs. hur de räknar med hundratavlan och om de hittar några regelmässigheter). Hundratavlan kan också utnyttjas senare vid addition och subtraktion. Då man adderar tiotal, rör man sig nedåt genom rutorna i tavlan. Då man subtraherar tiotal, rör man sig uppåt. Ental adderas genom att röra sig till höger och subtraheras genom att röra sig till vänster. Man kan även agera inom talområdet 0-200 genom att lägga två hundratavlor under varandra.
|
| Var är talet X? (den tomma hundratavlan) |
Läraren visar den tomma basen för hundratavlan och frågar: ”Var i hundratavlan är talet 27?” Barnet skriver talet i den tomma tavlan. Det är viktigt att fråga barnen hur de bestämt sig var talets plats ska vara. ”Var i hundratavlan är talet 37?” ”Och 57?” ”17?” Detta fortsätts tills alla tal som har 7 i platsen för ental har behandlats.
|
| Vilket tal har grannen? (hundratavlan samt ett papper med ett hål lika stor som en ruta i hundratavlan) |
Läraren sätter pappret på hundratavlan så att bara ett tal (t.ex. 35) syns genom hålet och ställer frågor: ”Vilket tal har grannen ovanför?” (25) ”Vilket tal har grannen nedanför?” (45) ”Vilket tal har grannen på höger sida?” (36) ”Vilket tal har grannen på vänster sida?” (34).
|
|
Lägga till, ta bort |
A) Lägga till. Läraren bildar ett tal som slutar på 9 eller 99, t.ex. 39, 249 eller 599. Barnet nämnar och skriver talet. Läraren ber barnet att lägga till en enbit eller en pinne i hopen samt att säga högt och skriva det nya talet. I övningen uppstår alltid ett nytt tiotal eller ett nytt hundratal, då barnet ska byta tio enheter mot en större enhet (t.ex. 10 enbitar mot en tiostav). Övningen kontrolleras genom att söka inledningstalet i hundratavlan och röra sig sedan ett steg framåt. Då det är fråga om tresiffriga tal kan flera hundratavlor användas: det jämna hundratalet kan läggas på bordet med baksidan upp. B) Ta bort. Övningen görs på samma sätt som övning A, men nu är inledningstalet något jämnt tiotal eller hundratal, t.ex. 50, 240 eller 600 och talet subtraheras med ett. |



